[NOIP2003] 提高组洛谷P1038 神经网络

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

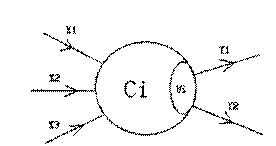
神经元〔编号为1）

图中，X1―X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。

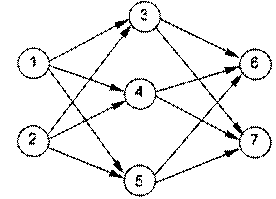
神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

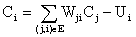
公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入输出格式

输入格式：

输入文件第一行是两个整数n（1≤n≤100）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

输出格式：

输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态，并且按照编号由小到大顺序输出！

若输出层的神经元最后状态均为 0，则输出 NULL。

输入输出样例

输入样例#1：

输出样例#1：

拓扑排序模拟传输即可。

每个神经元的C值可以直接减去阈值，等待活跃度大于0就可以传输。

但要注意，一开始有活跃度的是传入层，不能减去阈值（在这里WA了很久）

 #include<iostream>

 #include<cstdio>

 #include<algorithm>

 #include<cstring>

 #include<cmath>

 #include<queue>

 using namespace std;

 const int mxn=;

 int read(){

     int x=,f=;char ch=getchar();

     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}

     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}

     return x*f;

 }

 struct edge{

     int v,nxt;

     int dis;

 }e[];

 int hd[mxn],mct=;

 void add_edge(int u,int v,int dis){

     e[++mct].v=v;e[mct].dis=dis;e[mct].nxt=hd[u];hd[u]=mct;

     return;

 }

 int n,p;

 int c[mxn];

 int c1[mxn],c2[mxn];

 queue<int>q;

 bool inq[mxn];

 bool out[mxn];

 int main(){

     n=read();p=read();

     int i,j;

     int u,v;

     if(!p){

         u=read();v=read();

         printf("1 %d\n",u);

         return ;

     }

     for(i=;i<=n;i++){

         u=read();v=read();

         if(u){

             c[i]=u;q.push(i);

         }

         else c[i]=u-v;

     }

     for(i=;i<=p;++i){

         u=read();v=read();j=read();

         add_edge(u,v,j);

     }

     while(){

         for(i=;i<=n;i++){

             if(c[i]> && !inq[i] && hd[i]){

                 q.push(i);

                 inq[i]=;

             }

         }

         if(q.empty())break;

         int u=q.front();q.pop();inq[u]=;

         for(i=hd[u];i;i=e[i].nxt){

             int v=e[i].v;

             c[v]+=e[i].dis*c[u];

         }

         c[u]=;

     }

     bool flag=;

     for(i=;i<=n;i++){

         if(c[i]>)flag=,printf("%d %d\n",i,c[i]);

     }

     if(!flag)printf("NULL\n");

     return ;

 }