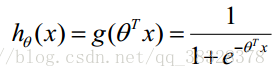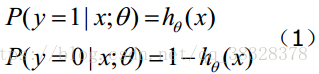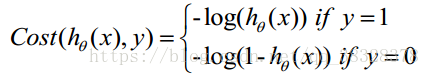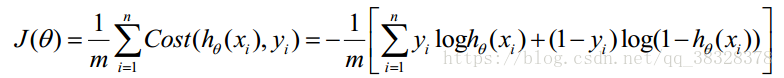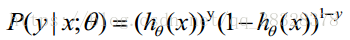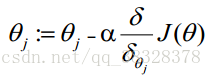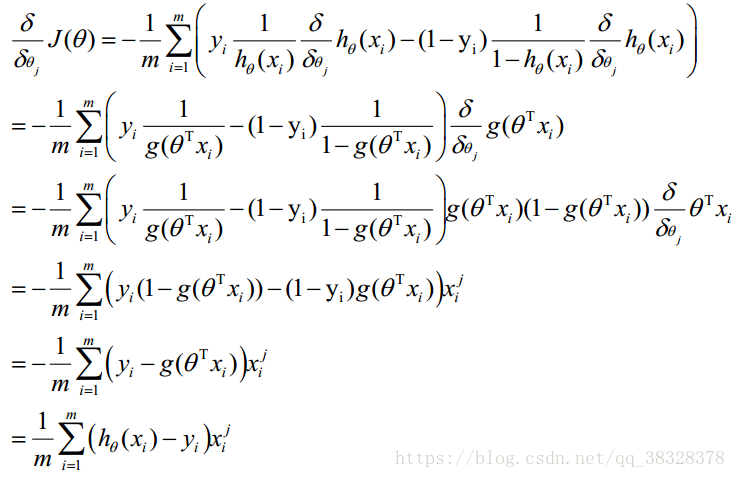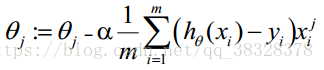Python机器学习算法 — 逻辑回归（Logistic Regression）

逻辑回归--简介

逻辑回归(Logistic Regression)就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。
        Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）。
        回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率。

逻辑回归--优缺点

优点： 
         1、速度快，适合二分类问题 ；
         2、简单易于理解，直接看到各个特征的权重 ；
         3、能容易地更新模型吸收新的数据 ；
 缺点：
         1、对数据的场景的适应能力有局限性，不如决策树算法适应性强；

逻辑回归--用途

用途：
        1、寻找危险因素：寻找某一疾病的危险因素等；
        2、预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；
        3、判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病

逻辑回归--原理

Logistic Regression和Linear Regression的原理是相似的，按照我自己的理解，可以简单的描述为这样的过程：
      （1）找一个合适的预测函数（Andrew Ng的公开课中称为hypothesis），一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程时非常关键的，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数。
      （2）构造一个Cost函数（损失函数），该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差。
      （3）显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有的是梯度下降法（Gradient Descent）。

逻辑回归--具体过程

一、构造预测函数

        Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

        Sigmoid 函数在有个很漂亮的“S”形，如下图所示：

下面左图是一个线性的决策边界，右图是非线性的决策边界：

对于线性边界的情况，边界形式如下：

构造预测函数为：

        函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

二、构造损失函数

Cost 函数和 J 函数如下，它们是基于最大似然估计推导得到的：

下面详细说明推导的过程：
        （1）式综合起来可以写成：

        取似然函数为：

        对数似然函数为：

        最大似然估计就是求使取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。但是，在Andrew Ng的课程中将 J(θ)  取为下式，即：

因为乘了一个负的系数-1/m，所以取 J(θ) 最小值时的θ为要求的最佳参数。

三、梯度下降法求的最小值

求J(θ)的最小值可以使用梯度下降法，根据梯度下降法可得θ的更新过程：

        式中为α学习步长，下面来求偏导：

        θ更新过程可以写成：

逻辑回归--实例

# -*- coding: utf-8 -*-

from numpy import *
import matplotlib.pyplot as plt

#从文件中加载数据：特征X，标签label
def loadDataSet():
    dataMatrix=[]
    dataLabel=[]
    #这里给出了python 中读取文件的简便方式
    f=open('testSet.txt')
    for line in f.readlines():
        #print(line)
        lineList=line.strip().split()
        dataMatrix.append([1,float(lineList[0]),float(lineList[1])])
        dataLabel.append(int(lineList[2]))
    #for i in range(len(dataMatrix)):
    #   print(dataMatrix[i])
    #print(dataLabel)
    #print(mat(dataLabel).transpose())
    matLabel=mat(dataLabel).transpose()
    return dataMatrix,matLabel

#logistic回归使用了sigmoid函数
def sigmoid(inX):
    return 1/(1+exp(-inX))

#函数中涉及如何将list转化成矩阵的操作：mat()
#同时还含有矩阵的转置操作：transpose()
#还有list和array的shape函数
#在处理矩阵乘法时，要注意的便是维数是否对应

#graAscent函数实现了梯度上升法，隐含了复杂的数学推理
#梯度上升算法，每次参数迭代时都需要遍历整个数据集
def graAscent(dataMatrix,matLabel):
    m,n=shape(dataMatrix)
    matMatrix=mat(dataMatrix)

    w=ones((n,1))
    alpha=0.001
    num=500
    for i in range(num):
        error=sigmoid(matMatrix*w)-matLabel
        w=w-alpha*matMatrix.transpose()*error
    return w

#随机梯度上升算法的实现，对于数据量较多的情况下计算量小，但分类效果差
#每次参数迭代时通过一个数据进行运算
def stocGraAscent(dataMatrix,matLabel):
    m,n=shape(dataMatrix)
    matMatrix=mat(dataMatrix)

    w=ones((n,1))
    alpha=0.001
    num=20  #这里的这个迭代次数对于分类效果影响很大，很小时分类效果很差
    for i in range(num):
        for j in range(m):
            error=sigmoid(matMatrix[j]*w)-matLabel[j]
            w=w-alpha*matMatrix[j].transpose()*error
    return w

#改进后的随机梯度上升算法
#从两个方面对随机梯度上升算法进行了改进,正确率确实提高了很多
#改进一：对于学习率alpha采用非线性下降的方式使得每次都不一样
#改进二：每次使用一个数据，但是每次随机的选取数据，选过的不在进行选择
def stocGraAscent1(dataMatrix,matLabel):
    m,n=shape(dataMatrix)
    matMatrix=mat(dataMatrix)

    w=ones((n,1))
    num=200  #这里的这个迭代次数对于分类效果影响很大，很小时分类效果很差
    setIndex=set([])
    for i in range(num):
        for j in range(m):
            alpha=4/(1+i+j)+0.01

            dataIndex=random.randint(0,100)
            while dataIndex in setIndex:
                setIndex.add(dataIndex)
                dataIndex=random.randint(0,100)
            error=sigmoid(matMatrix[dataIndex]*w)-matLabel[dataIndex]
            w=w-alpha*matMatrix[dataIndex].transpose()*error
    return w

#绘制图像
def draw(weight):
    x0List=[];y0List=[];
    x1List=[];y1List=[];
    f=open('testSet.txt','r')
    for line in f.readlines():
        lineList=line.strip().split()
        if lineList[2]=='0':
            x0List.append(float(lineList[0]))
            y0List.append(float(lineList[1]))
        else:
            x1List.append(float(lineList[0]))
            y1List.append(float(lineList[1]))

    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(x0List,y0List,s=10,c='red')
    ax.scatter(x1List,y1List,s=10,c='green')

    xList=[];yList=[]
    x=arange(-3,3,0.1)
    for i in arange(len(x)):
        xList.append(x[i])

    y=(-weight[0]-weight[1]*x)/weight[2]
    for j in arange(y.shape[1]):
        yList.append(y[0,j])

    ax.plot(xList,yList)
    plt.xlabel('x1');plt.ylabel('x2')
    plt.show()

if __name__ == '__main__':
    dataMatrix,matLabel=loadDataSet()
    #weight=graAscent(dataMatrix,matLabel)
    weight=stocGraAscent1(dataMatrix,matLabel)
    print(weight)
    draw(weight)