codeforces 414B B. Mashmokh and ACM(dp)

题目链接：

B. Mashmokh and ACM

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mashmokh's boss, Bimokh, didn't like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh's team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn't able to solve them. That's why he asked you to help him with these tasks. One of these tasks is the following.

A sequence of l integers b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally 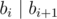 for all i (1 ≤ i ≤ l - 1).

Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007(10^9 + 7).

Input

 

The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).

Output

 

Output a single integer — the number of good sequences of length k modulo 1000000007 (10^9 + 7).

Examples

 

input

3 2

output

5

input

6 4

output

39

input

2 1

output

2

Note

In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].

题意：

给出这么多数[1,n],问能形成长为l的数列满足b[i]|b[i+1]的方案数;

思路：

dp[i][j]表示长为i,以j结尾的方案数,

dp[i+1][j]=∑dp[i][k],k为j的因数;

AC代码：

#include <bits/stdc++.h>
using namespace std;
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef long long LL;
const LL mod=1e9+;
const double PI=acos(-1.0);
const int inf=0x3f3f3f3f;
const int N=2e5+;
LL dp[][];
int main()
{
        int n,k;
        scanf("%d%d",&n,&k);
        for(int i=;i<=n;i++)
        {
            dp[][i]=;
        }
        for(int i=;i<=k;i++)
        {
            Rjep(n)
            {
                for(int x=;x*j<=;x++)
                {
                    dp[i+][x*j]+=dp[i][j];
                    dp[i+][x*j]%=mod;
                }
            }
        }
        LL ans=;
        for(int i=;i<=n;i++)
        {
            ans+=dp[k][i];
            ans%=mod;
        }
        cout<<ans<<"\n";
 
    return ;
}