Spherical Harmonics Lighting
【转自:http://www.cnblogs.com/daniagger/archive/2012/05/29/2524133.html】
1、背景知识
1.1 光照表示
之前我们都只考虑光源点和物体表面点的光照作用,而现在,我们考虑物体表面点延伸的微型平面,这个微型平面作为半球形的底部,因此光照射进来的范围就是整个半球形,这也是BRDF的基础。
1.2 数据压缩
对于压缩信号来说,很多压缩技术基于这样一个思路:使用不同基函数的不同组合来组成一个更为复杂的数字信号表示。
保存数字信号的最繁琐方法是保存每一个数据点,然而一个复杂的信号可能有成千上万个点,所以需要找到方法来压缩。对于每一个基函数,我们用频率(frequency),振幅(amplitude)和相位(phase)来表示,这三个数被称为系数(coefficient),这样就大大减小了数据量。
在现实生活中,数字信号并不能很明显的表示成多个基函数的组合,很多例子中,系数的个数和原始数据点的个数相差无几,所以要找寻其他压缩方法。人们要寻找信号中那些信息是最为重要的,有些信息可能是噪声,这些信息需要被剔除出去。
基函数是这样一种函数,可以被裁剪和组合,来模拟任何一种数学函数。裁剪因子通常被称为系数(coefficient)。举个例子,如果要通过基函数组Bi(x)来模拟函数f(x),ci是对应的系数。
公式如下图:
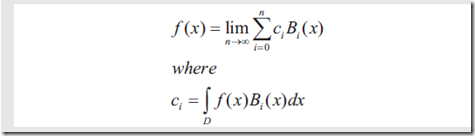
这也就是傅里叶变换。
1.3 光照信息的压缩
对于diffuse lighting来说,高频率的部分需要被剔除。
2、SH的定义
Spherical harmonics是可以重构任何函数的基函数,研究二维函数的单位球。
SH是定义在单位球表面的基函数,表示在球面坐标下。
球坐标系
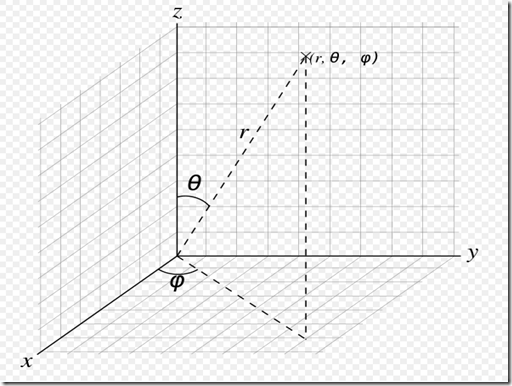
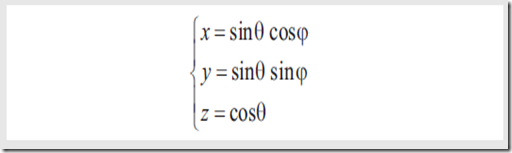
其中r=1。
SH的一般形式是
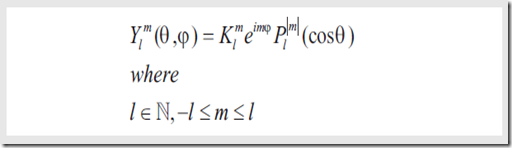
实际形式,也就是接下来会用到的形式是
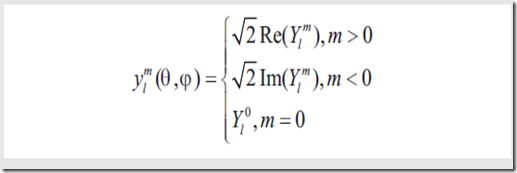
最终形式是
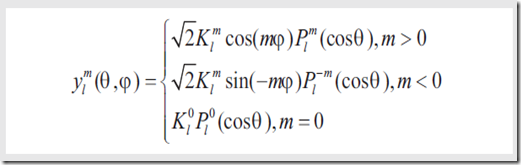
公式中的项:
Plm是勒让德多项式,定义在[-1,1]范围内,递归式是

Klm是用来将函数规范化的裁剪因子,定义式是
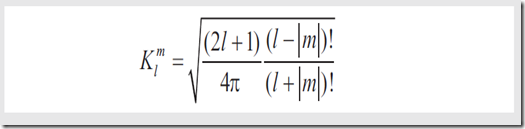
SH的简化形式为(二维变一维)
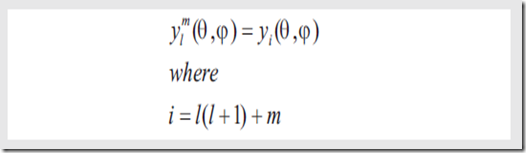
3、构造
由SH基函数模拟的函数是
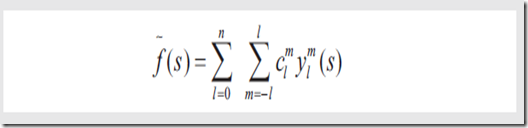
其中
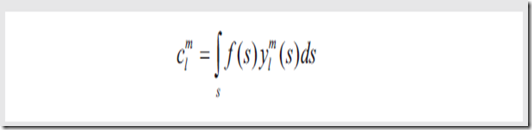
上面的函数是原始函数的限制带宽版,原始函数表示为
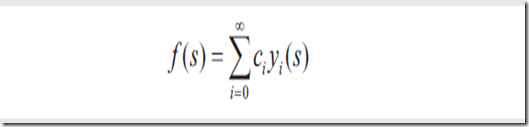
使用SH的简化形式,则模拟的函数为
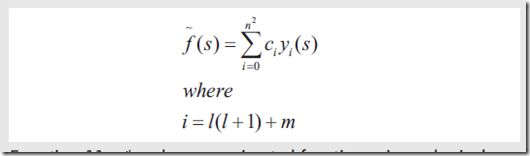
使用Monte Carlo积分算法,可以求出系数为
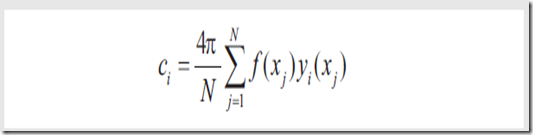
对于用SH构造的函数,你需要将单位球划分为n x n个样品,对于每一个系数,遍历所有的样品,应用上面的公式。最终可以得到所有系数的表达式。
4、SH的性质
4.1 正交性
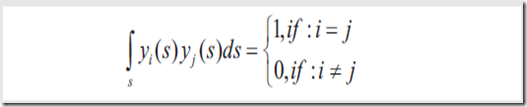
4.2
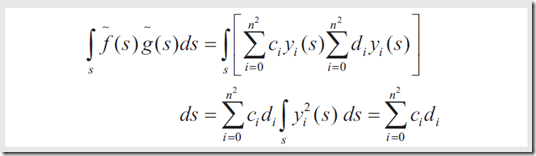
4.3
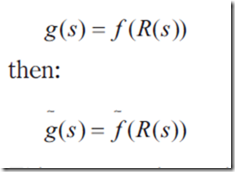
5、SH应用到光照上
5.1 光照方程
最常用的光照方程是
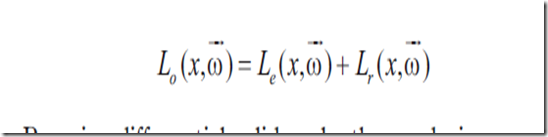
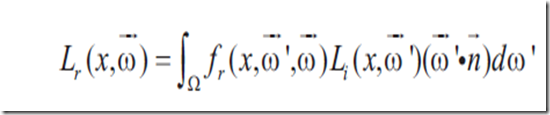
Lo是表面顶点x在w方向上发出的光照度,其中w'是入射光线,由自发光部分(Le)和反射部分(Lr)组成,Lr的积分是对半球范围内所有的光线进行积分。
通过使用differential solid angle,光照方程可表示为
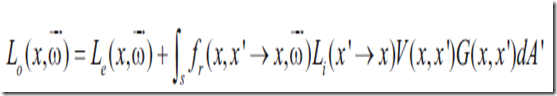
反射分量是对S中所有点的积分,入射光线从x’到x,V是x和x’之间可见度方程,G是几何项。V返回布尔值(如果x和x’相互可见,则返回1),几何项则依赖于表面点x和x’之间的几何关系。
该积分不能实时计算出来,所以需要预处理这个积分,利用性质2。
预处理步骤:
a、将入射光线投影到SH基上。入射光线需要表示成球坐标方程。
b、对于物体上的每一个点,将BRDF项、可见项、几何项的乘积投影到SH基上。该乘积也被当做转移方程。
实时积分项可以通过计算转移方程的SH系数和入射光线的SH系数的点积而得到,即利用性质2,将入射光线当成复合函数,BRDF项可见项几何项的乘积当做另一个复合函数,原始积分也就是两个复合函数乘积的积分。
同时,取样点分布在n x n的方形网格上,投影到球坐标系
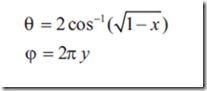
现在我们需要简化光照方程,我们不考虑自发光,并且反射光线均匀分布在所有方向,BRDF是一个常量,最终我们得到
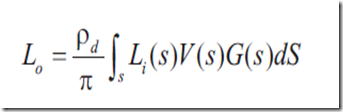
6、SH Diffuse Lighting
不考虑阴影的情况下(V项恒为1),特定点的diffuse lighting为
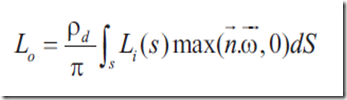
现在需要求入射光线的SH投影和cosine项(即转移方程)的SH投影,两者都用Monte Carlo积分法,这些都在预处理步完成。运行时,特定点的光照计算使用上述公式(将两个SH系数求点积)。
7、SH Diffuse Shadowed Lighting
现在需要考虑V项
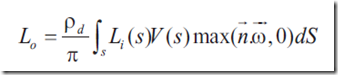
新的转移方程变成了
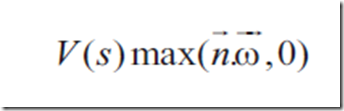
要确定V项,需要从当前顶点追踪射线到场景中,如果射线和一个三角面片相交,则光线被阻挡。
8、SH Diffuse Shadowed Inter-Reflected Lighting
现在,不仅要考虑从光源发出来的光线,还要考虑在场景中互相作用的光线。也就是全局光照。简化了的光照方程如下
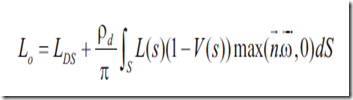
Spherical Harmonics Lighting的更多相关文章
- 球谐光照(Spherical Harmonics Lighting)及其应用-实验篇
简介 之前在一篇实时深度图优化的论文中看到球谐光照(Spherical Harmonics Lighting)的应用,在查阅了许许多多资料之后还是无法完全理解,我个人觉得如果之前对实时渲染技术不是很了 ...
- 球谐光照(Spherical Harmonics Lighting)及其应用-应用篇
上一篇介绍了球谐函数的一些原理和性质,本篇主要介绍如何实现球谐光照,将这种光照应用到实际的场景中去. 我们知道,球谐光照实际上就是将周围的环境光采样成几个系数,然后渲染的时候用这几个系数来对光照进行还 ...
- Luckily general gradient for spherical harmonics is defined
http://web4.cs.ucl.ac.uk/staff/j.kautz/publications/gradientSH_RS04.pdf
- Thinking in Unity3D:渲染管线中的Rendering Path
关于<Thinking in Unity3D> 笔者在研究和使用Unity3D的过程中,获得了一些Unity3D方面的信息,同时也感叹Unity3D设计之精妙.不得不说,笔者最近几年的 ...
- Physically Based Shader Development for Unity 2017 Develop Custom Lighting Systems (Claudia Doppioslash 著)
http://www.doppioslash.com/ https://github.com/Apress/physically-based-shader-dev-for-unity-2017 Par ...
- SRBF Lighting
SRBF的全称是Spherical Radial Basis Function,笔者擅自翻译为球面放射基底函数.由于SRBF并不怎么出名,相对来说,SH(Spherical Harmonic)球 ...
- Image Based Lighting In UE3
"IBL"全称为"Image-based Lighint",是一种伪装全局光照的方法.使用该方法可以获得较好的视觉效果并且可以达到实时渲染的目的. 实现的方法之 ...
- [我给Unity官方视频教程做中文字幕]beginner Graphics – Lessons系列之灯光介绍Lights
[我给Unity官方视频教程做中文字幕]beginner Graphics – Lessons系列之灯光介绍Lights 既上一篇分享了中文字幕的摄像机介绍Cameras后,本篇分享一下第2个已完工的 ...
- Computer Graphics Research Software
Computer Graphics Research Software Helping you avoid re-inventing the wheel since 2009! Last update ...
随机推荐
- linxu下的shell脚本加密,shell生成二机制可执行文件
再安全的加密也抵不过逆向,斗智斗勇吧,持续加密持续破解 1.简单的加密:gzexe file.sh 2.使用shc加密:下载地址:http://www.datsi.fi.upm.es/~frosal/ ...
- BUPT复试专题—排序(2009)
题目描述 查找序列a 中小于 b 的第 i 个数的数的个数 输入 输入有多组,每组四行第一行:序列a个数N第二行:(序列a的)N个数,升序排列第三行:序列b个数M 第四行:(序列b的)M个数,升序排列 ...
- BMP文件的读取与显示
有三个函数能够完毕这一功能 1.BitBlt BitBlt 用于从原设备中复制位图到目标设备 void CMFCApplication1View::OnDraw(CDC* pDC) { CMFC ...
- gulp - sass 插件一直安装不好?
1.没有sass,只存在与scss 任务 gulp.task('scss', function() { return gulp.src(app.srcPath + '/sass/*.scss') .p ...
- 消息列队 php 基于redis 实现
说明 消息列队 基于PHP 实现. 之前 用python 的 flower 实现了 列队. 今天这里我们用的是 PHP 来实现: 在实际的业务环境中 PHP 用的多些: PHP 实现列队 最重要的是用 ...
- jQuery的ajax,当async为false时,同步操作失败。解决方式
引发失败时代码: $.ajax({ url : 'your url', data:{name:value}, cache : false, async : true, type : "POS ...
- SQL server创建和管理
数据库函数的应用 数据库的查询方法 修改和替换数据库的数据
- Sublime Text使用
安装Sublime Text Sublime 的安装比較简单,我们能够直接去官网http://www.sublimetext.com/,点击Download菜单.进入之后选择自己操作系统的进行下载安装 ...
- Intel processor brand names-Xeon,Core,Pentium,Celeron----Pentium
http://en.wikipedia.org/wiki/Pentium Pentium From Wikipedia, the free encyclopedia This article ...
- 聊聊高并发(三十二)实现一个基于链表的无锁Set集合
Set表示一种没有反复元素的集合类,在JDK里面有HashSet的实现,底层是基于HashMap来实现的.这里实现一个简化版本号的Set,有下面约束: 1. 基于链表实现.链表节点依照对象的hashC ...
