【VHDL】深度讲解二进制无符号和有符号加法处理溢出的问题

1.Unsigned adders

这个比较简单，只需在A、B前面扩展一位0防止溢出，溢出的数填到第n位cout，n-1到0位就是sum。

，

2.Signed adders

一开始也搞不懂下图中为什么要扩展符号位，两个符号位了怎么加？   往下看↓

2.1 Analysis

在真正开始使用Verilog做signed加法运算前，我们先来看看实际上二进制singed加法是如何运算?

Normal Condition (没有Overflow)

(+6) + (-3) = (+3)

为了节省resource，我们故意使用4 bit的+6与3 bit的-3相加，若直接将两个signed值相加，答案为-7，很显然答案并不正确。

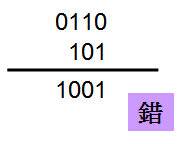
因为4 bit与3 bit相加，结果可能进位到5 bit，正确的作法是将4 bit的+6做signed extension到5 bit，且3 bit的-3也要做signed extension到5 bit后，然后才相加，若最后进位到6 bit，则不考虑6 bit的值。

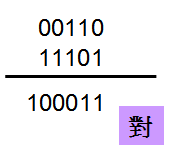
在此补充一下何谓Singed Extension?简单的说，当以较多bit显示signed型态的值时，重复signed bit补齐。

就意义上来说，就是3 bit的signed值若要以5 bit表示时，必须补上signed bit才能在5 bit表示，所以101要变成11101。

Boundary Condition (正Overflow)

(+7) + (+3) = (+10)

为了节省resource，我们一样故意使用4 bit的+7与3 bit的+3相加，若直接将两个signed值相加，答案为-6，很显然答案并不正确。

根据上个例子的经验，+7与+3必须做signed extension才能相加，这样才能得到正确答案+10。

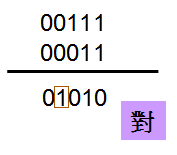
不过现在问题来了，+10必须动到5 bit才能显示，若输出的值域为4 bit，只能-8 ~ +7，+10很显然已经正overflow了‧

若只能以4 bit表示，因为是正的，MSB必须是0(SUM[3]=0)，所以若MSB是1就表示由进位而来，也就是正overflow了(此例的SUM[3]为1，所以已经正overflow)，再加上因为目前运算结果为5 bit，且是正，所以SUM[5]必须为0。

也就是说，若SUM[5]=0且SUM[4]=1时，为正overflow，所以01010对于4 bit来说，是正overflow。

Boundary Condition (负Overflow)

(-5) + (-4) = (-9)

同样为了节省resource，我们故意使用4 bit的-5与3 bit的-4相加，若直接将两个signed值相加，答案为-1，很显然的答案并不正确。

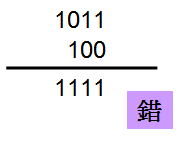
根据前面两个例子，-5与-4一样必须做signed extension才能相加，这样才能得到正确答案-9‧进位到6 bit的1要舍去，所以答案是10111‧

问题一样来了，-9必须动到5 bit才能显示，若输出的值域是4 bit，只能-8 ~ +7，-9很显然已经是负overflow了。

若只能以4 bit表示，因为是负的，MSB必须是1(SUM[3]=1)，所以若MSB是0就表示由进位而来，也就是负overflow了(此例的SUM[3]为0，所以已经负overflow)，再加上因为目前运算结果为5 bit，且是负，所以SUM[5]必须为1‧

也就是说，若SUM[5]为1且SUM[4]为0时，为负overflow，所以10111对于4 bit来说，是负overflow。

2.2 Summary

根据之前三个实际的例子，我们得到以下结论：

m bit + m bit =< (m+1) bit m bit + n bit =< (m+1) bit，其中n < m ul style='list-style:disc outside none;' > m bit与n bit都必须先做signed extension到(m+1) bit才能相加 若结果有到(m+2) bit则忽略之，实际的结果为(m+1) bit 若Sum[m+1] ^ Sum[m]为1，表示有overflow 若Sum[m+1]为0且Sum[m]为1，则为正overflow 若Sum[m+1]为1且Sum[m]为0，则为负overflow

[1]如何实现有符号无符号加减法，如何处理overflowhttp://www.eeskill.com/article/id/45756