（4）主成分分析Principal Component Analysis—

主成分分析Principal Component Analysis

降维除了便于计算，另一个作用就是便于可视化。

主成分分析-->降维-->

方差：描述样本整体分布的疏密，方差越大->样本越稀疏，方差越小->样本越紧密

所以问题转化成了 -->

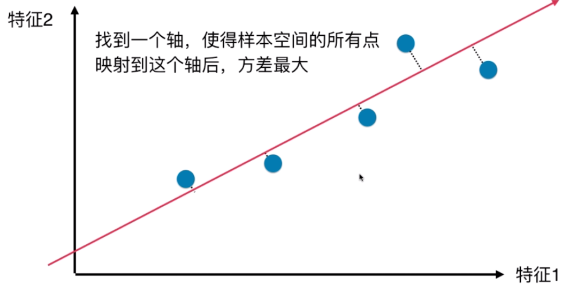
与线性回归对比，似乎有些类似。但它们是不同的！

不仅是公式上有区别，且对于线性回归来说，其纵轴轴对应的是输出标记。而PCA中其两个轴都是表示特征。

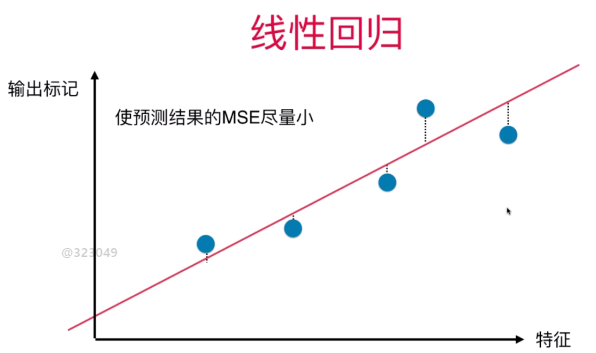
且这些点是垂直于特征轴，而不是红线轴

PCA第一步：将样例的均值归为0（demean），即在每个维度上的均值为0，如下图，

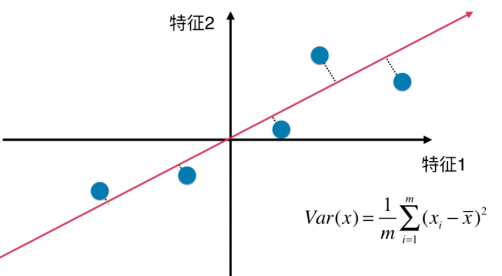
因此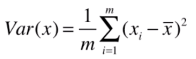，可化为，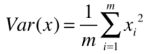

对于该式，X⁽ⁱ⁾ 是所有样本点已经映射到新的坐标轴上之后，得到的新的样本，蓝点。

步骤-->

1. 对所有样本进行demean处理

2. 求一个轴的方向 w = (w₁, w₂)

3. 使得所有样本映射到w以后，有：

最大

映射后样本方差 = （映射后每一个样本 i 的值 - 映射后整体均值）的平方和 / m

注意：对X可能有n个维度，即使对于二维，每一个样本本身也是包含有2个数的向量。所以，该式更应该表示成以下形式：

（双杠表示模）

X_project_bar = X_bar （他俩平均值其实是一样的）

又因为我们已经进行了demean处理，其平均值为0，有，

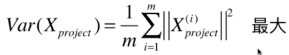----------（1）

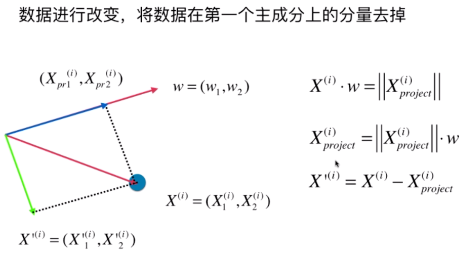
假设红线代表我们要找的方向 w = (w₁, w₂)，蓝色的样本点对应X中的第 i 行 X⁽ⁱ⁾ = (X₁⁽ⁱ⁾ , X₂⁽ⁱ⁾), X⁽ⁱ⁾ 此时也是一个向量。 X⁽ⁱ⁾ 映射到 w 上，即向w表示的轴做一个垂线，有交点，交点位置的这一点即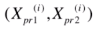

要求模的平方，其实就是求蓝色轴的长度对应的平方

也可理解成，把一个向量映射到另一个向量上，对应的映射长度是多少。实际上这种映射就是点乘的定义。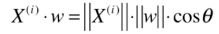，两个红线的夹角即西塔。

由于要找的 w 是一个轴，它是一个方向，可用方向向量来表示，即 w 的模为 1. 因此上式可化简为，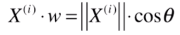

此时X⁽ⁱ⁾ 的模是表示X⁽ⁱ⁾ 的向量对应的长度，再乘以 cos西塔，得到的就是蓝色向量的长度。即，

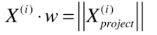
因此（1）式可化简为，

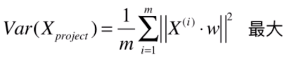
由于两个向量点乘是一个数，所以可以不用取模的符号了，即

梯度上升法求解PCA问题

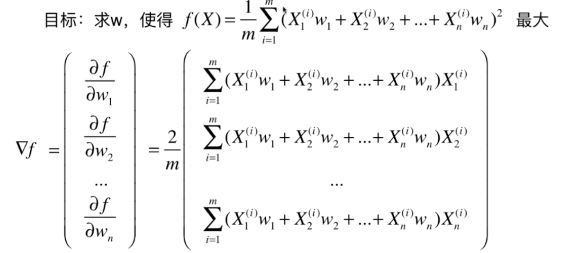
与线性回归中推导的公式很像，可化成，

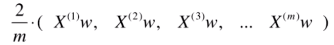与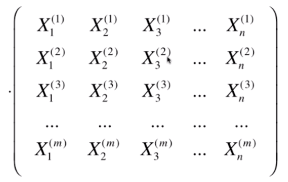这个矩阵相乘，即，

注，Xw 本身是(m* n) * (n*1) = m * 1 的列向量。在这里我们写成行向量的形式，所以做了一个转置。又因为得到的结果 (1*m) * (m*n) = 1 * n 的行向量，而我们其实想要的是 n*1 的梯度。所以我们再对整个结果做一个转置，即，

（注：（A*B）的转置 = B的转置乘以A的转置）

铛铛！得到向量化的结果啦！

求数据的前n个主成分

主成分分析：一组坐标系转移到另一组坐标系，进行重新排列。原先n维特征n个轴，转移后仍然是n个轴。使得其在第一个轴上方差最大，第二个轴次之，以此类推。

求出第一主成分后，如何求出下一个主成分？

高维数据向低维数据映射

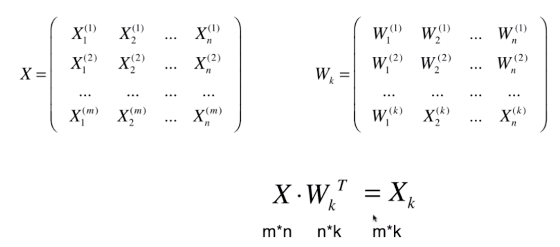
第一个样本X(1)和w(1)相乘，就是第一个数据在第一个主成分上的映射。W(1)也有n维，是因为原来的X中每个样本都是n维，所以转换后也还是在一个n维的空间中。

但我们将原来m*n 维降到了 m*k维，k 表示前k个主成分。（k<n）。完成了高维数据到低维数据的映射。

也可完成从低维恢复到高维，用Xk中每一行乘以 Wk 每一列。 (m*k) * (k*n) = m*n

但这也是不可能恢复的和原数据一样，因为降维的过程中丢失了一些数据。