P1265 公路修建洛谷

https://www.luogu.org/problem/show?pid=1265

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式

输入格式：

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

输出格式：

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

输入输出样例

输入样例#1：

输出样例#1：

6.47

说明

修建的公路如图所示：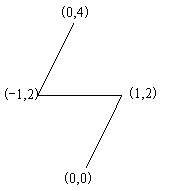

很容易发现，特殊情况没什么用，唬人的~~~、

表示我无奈的一zui代码~

 #include <algorithm>

 #include <iostream>

 #include <cstdio>

 #include <cmath>

 #define N 5233

 #define maxn 1e7

 using namespace std;

 int minn,k;

 bool vis[N];

 int n,x[N],y[N];

 double d[N],ans;

 double dis[N][N];

 void Prime()

 {

     for(int i=;i<=n;i++) d[i]=dis[][i];

     d[]=;vis[]=;

     for(int i=;i<n;i++)

     {

         minn=maxn;

         for(int j=;j<=n;j++)

             if(!vis[j]&&minn>d[j])

             {

                 minn=d[j];

                 k=j;

             }

         vis[k]=;

         for(int j=;j<=n;j++)

             if(!vis[j]&&d[j]>dis[k][j])

             d[j]=dis[k][j];

     }

 }

 int main()

 {

     scanf("%d",&n);

     for(int i=;i<=n;i++)

         cin>>x[i]>>y[i];

     for(int i=;i<=n;i++)

         for(int j=;j<=n;j++)

             dis[i][j]=sqrt(pow((x[i]-x[j]),)*1.0+pow((y[i]-y[j]),)*1.0);

     Prime();

     for(int i=;i<=n;i++)

         ans+=d[i];

     printf("%.2lf",ans);

     return ;

 }

80分，TLE两个（最朴素的Prime）

 #include <algorithm>

 #include <iostream>

 #include <cstdio>

 #include <cmath>

 #define N 5233

 #define maxn 1e7

 using namespace std;

 bool vis[N];

 double minn;

 double d[N],ans;

 int n,x[N],y[N],k;

 double count(int i,int j)

 {

     return sqrt(pow((x[i]-x[j]),)*1.0+pow((y[i]-y[j]),)*1.0);

 }

 int main()

 {

     scanf("%d",&n);

     for(int i=;i<=n;i++)

         scanf("%d%d",&x[i],&y[i]);

     for(int i=;i<=n;i++) d[i]=count(,i);

     d[]=;vis[]=;

     for(int i=;i<n;i++)

     {

         minn=maxn;

         for(int j=;j<=n;j++)

             if(!vis[j]&&minn>d[j])

             {

                 minn=d[j];

                 k=j;

             }

         vis[k]=;ans+=minn;

         for(int j=;j<=n;j++)

         {

             double cnt=count(k,j);

             if(!vis[j]&&d[j]>cnt)

             d[j]=cnt;

         }

     }

     printf("%.2lf",ans);

     return ;

 }

80分，TLE两个（不用二维数组存图）

 #include <algorithm>

 #include <iostream>

 #include <cstdio>

 #include <cmath>

 #define N 5233

 #define maxn 1e7

 using namespace std;

 int minn,k;

 bool vis[N];

 int n,x[N],y[N];

 double d[N],ans;

 double count(int i,int j)

 {

     return sqrt(pow((x[i]-x[j]),)*1.0+pow((y[i]-y[j]),)*1.0);

 }

 void Prime()

 {

     for(int i=;i<=n;i++) d[i]=count(,i);

     d[]=;vis[]=;

     for(int i=;i<n;i++)

     {

         minn=maxn;

         for(int j=;j<=n;j++)

             if(!vis[j]&&minn>d[j])

             {

                 minn=d[j];

                 k=j;

             }

         vis[k]=;

         for(int j=;j<=n;j++)

         {

             double cnt=count(k,j);

             if(!vis[j]&&d[j]>cnt)

             d[j]=cnt;

         }

     }

 }

 int main()

 {

     scanf("%d",&n);

     for(int i=;i<=n;i++)

         cin>>x[i]>>y[i];

     Prime();

     for(int i=;i<=n;i++)

         ans+=d[i];

     printf("%.2lf",ans);

     return ;

 }

90分，TLE一个（小优化）

 #include <algorithm>

 #include <iostream>

 #include <cstdio>

 #include <cmath>

 #define N 5233

 #define maxn 1e7

 using namespace std;

 bool vis[N];

 double minn,cnt;

 double d[N],ans;

 int n,x[N],y[N],k;

 double count(int i,int j)

 {

     return sqrt((double)(x[i]-x[j])*(x[i]-x[j])+(double)(y[i]-y[j])*(y[i]-y[j]));

 }

 int main()

 {

     scanf("%d",&n);

     for(int i=;i<=n;i++)

         scanf("%d%d",&x[i],&y[i]);

     for(int i=;i<=n;i++) d[i]=count(,i);

     d[]=;vis[]=;

     for(int i=;i<n;i++)

     {

         minn=maxn;

         for(int j=;j<=n;j++)

             if(!vis[j]&&minn>d[j])

             {

                 minn=d[j];

                 k=j;

             }

         vis[k]=;ans+=minn;

         for(int j=;j<=n;j++)

         {

             cnt=count(k,j);

             if(!vis[j]&&d[j]>cnt)

             d[j]=cnt;

         }

     }

     printf("%.2lf",ans);

     return ;

 }

稀里哗啦改了一通~~~AC

恶心~~~