dp之斜率优化

前几天想练练思维，所以从cf上随便找了一道dp题，看完题意后第一感觉很简单，就是简单的区间dp题，但是看到数据范围的我顿时就懵了，（1≤n≤10⁵）

emmmmmmmm，按照普通的思路肯定会超时的。。。。

想了很久，总感觉可以利用前面已经经历过的点进行优化，但是不知道该怎么动手

问了度娘后发现这题需要用到单调栈还是斜率优化之类的。。。。。

额。。。之前听说过斜率优化，但是没有真正的学习过，然后找了网上大佬的博客学习了一番，终于学会了一点皮毛

https://www.cnblogs.com/ka200812/archive/2012/08/03/2621345.html

这位大佬给的图好像反了。。。但是讲解非常的通俗易懂

https://blog.csdn.net/lxc779760807/article/details/51366552

https://www.cnblogs.com/orzzz/p/7885971.html

大米饼：https://www.cnblogs.com/Paul-Guderian/p/7259491.html

做完大米饼大佬博客推荐的题目后，我总结了一点经验

我们遇到斜率优化dp时，和其他dp一样，首先我们要推出它的状态转移方程,例如

f[i]=min(f[j]+add(i,j))(j<i)

然后将状态转移方程转化为

y   =   kx   +   b     的形式

只与j有关  k只与i有关  我们要求的f[i]

x只与j有关

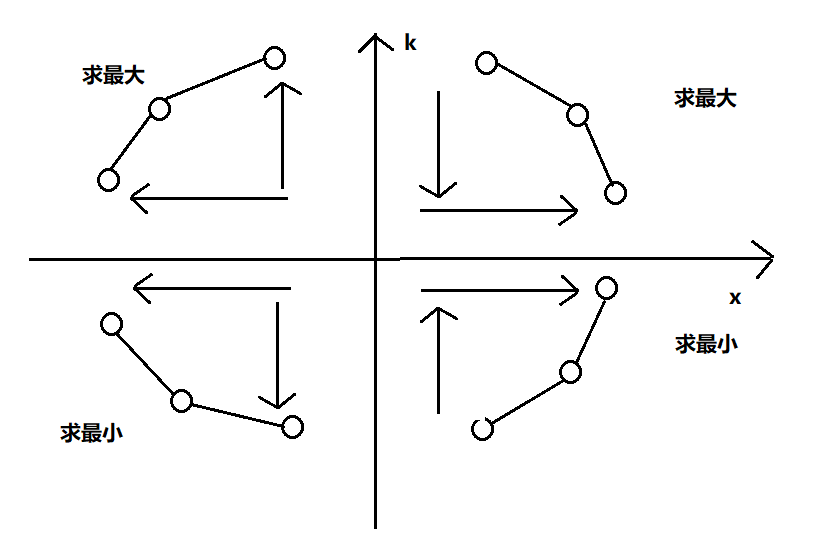
然后根据x的单调性和k的正负判断该建立一个怎样的凸包（用排列组合算有八种（2³），但是我只确定了四种的，以后再补充吧）