【NOIP2015提高组】 Day1 T2 信息传递

题目描述

有n个同学（编号为1到n）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为i的同学的信息传递对象是编号为Ti同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息，但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

输入共2行。

第1行包含1个正整数n表示n个人。

第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i

的同学的信息传递对象是编号为Ti的同学，Ti≤n且Ti≠i

数据保证游戏一定会结束。

输出格式：

输出共 1 行，包含 1 个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：

5
2 4 2 3 1

输出样例#1：

3

说明

样例1解释

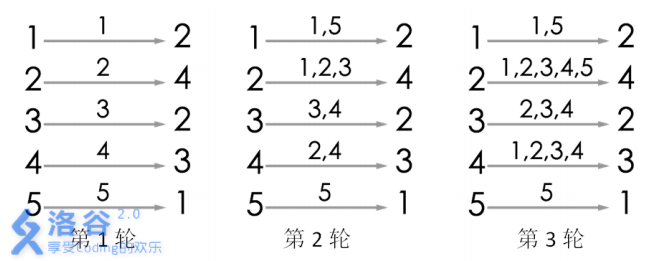
游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自

己的生日，所以答案为 3。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息

来源得知自己的生日，同样符合游戏结束的条件。

对于 30%的数据， n ≤ 200；

对于 60%的数据， n ≤ 2500；

对于 100%的数据， n ≤ 200000。

题解：

不难看出，题目要求的是该图中包含点数最少但点数≥2的环所包含的点数。

直接对于每个点进行dfs求最小的环即可

但这种做法是O（n^2）的，考虑到n≤500,000，故需进行优化

考虑到题目中所求环为最小，那么当搜索到一个点在上一轮已经被遍历过时，其必找到另一个环，则不用向该点继续搜索。故每个点有且只有被遍历一次，时间复杂度为O(n)

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<stack>
 #define M 210000
 #define INF 123123123
 using namespace std;
 int nx[M]={},n,vis[M]={},t=;
 bool b[M]={};
 stack<int> s;
 int bfs(int x){
     vis[x]=++t;
     if(nx[x]==x) return INF;
     b[x]=; s.push(x);
     while(!vis[nx[x]]){
         x=nx[x];
         vis[x]=++t;
         b[x]=; s.push(x);
     }
     if(b[nx[x]]){
         while(!s.empty()) b[s.top()]=,s.pop();
         return vis[x]-vis[nx[x]]+;
     }else{
         while(!s.empty()) b[s.top()]=,s.pop();
         return INF;
     }
 }

 int main(){
     freopen("message.in","r",stdin);
     freopen("message.out","w",stdout);
     scanf("%d",&n); int minn=INF;
     for(int i=;i<=n;i++) scanf("%d",nx+i);
     for(int i=;i<=n;i++) if(!vis[i])
     minn=min(minn,bfs(i));
     cout<<minn<<endl;
 }