HDU 3625 Examining the Rooms：第一类stirling数

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3625

题意：

　　有n个房间，每个房间里放着一把钥匙，对应能开1到n号房间的门。

　　除了1号门，你可以踹开任意一扇门（不用钥匙），但你最多只能踹k次。

　　问你能将所有门打开的概率。

题解：

　　· P(打开所有门) = 能打开所有门的钥匙放置情况数 / 钥匙放置的总情况数

　　· 钥匙放置的总情况数 = n!

　　

　　那么考虑下能打开所有门的钥匙放置情况数。。。

　　由于每个房间里有且只有一把钥匙，所以如果将每个房间连向房间内钥匙对应的房间，会得到一个有向图，并且由若干个独立的环组成。

　　

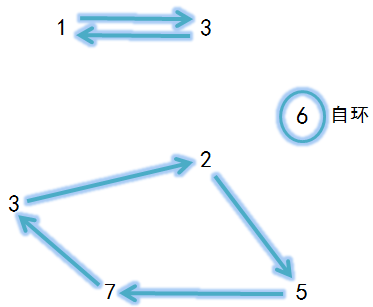
　　所以，只要将一个环内的任意一扇门踹开，就能打开这个环上的所有房间。

　　如果不考虑1号门，那么要算的就是n个元素组成1~k个环排列的情况数。

　　第一类Stirling数的定义啊！

　　递推式：s(n,k) = s(n-1,k-1) + (n-1)*s(n-1,k)

　　

　　So...

　　· 能打开所有门的钥匙放置情况数 = ∑S(n,i)　(1<=i<=k)

　　

　　考虑到1号门不能踹，也就是1不能独立成环，它的情况数就等于用剩下n-1的元素组成i-1个环的情况数。

　　· 能打开所有门的钥匙放置情况数 = ∑( S(n,i)-S(n-1,i-1) )

　　所以答案为：∑( S(n,i)-S(n-1,i-1) ) / n!　　(1<=i<=k)

AC Code:

 // s(n,k) = s(n-1,k-1) + (n-1)*s(n-1,k)
 // s(n,0) = 0    s(n,n) = 1
 // P = sigma(s[n][i]-s[n-1][i-1])/fact(n)    1<=i<=k

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #define MAX_N 25
 #define MAX_K 25

 using namespace std;

 int n,k,t;
 long long sum;
 long long s[MAX_N][MAX_K];
 long long fact[MAX_N];

 void stirling()
 {
     memset(s,,sizeof(s));
     for(int i=;i<MAX_N;i++)
     {
         s[i][i]=;
         for(int j=;j<i;j++)
         {
             s[i][j]=s[i-][j-]+(i-)*s[i-][j];
         }
     }
 }

 void cal_fact()
 {
     fact[]=;
     for(int i=;i<MAX_N;i++)
     {
         fact[i]=fact[i-]*i;
     }
 }

 int main()
 {
     stirling();
     cal_fact();
     cin>>t;
     for(int cas=;cas<=t;cas++)
     {
         cin>>n>>k;
         sum=;
         for(int i=;i<=k;i++)
         {
             sum+=s[n][i]-s[n-][i-];
         }
         printf("%.4f\n",(double)sum/fact[n]);
     }
 }