poj 1759 Garland

Garland

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2365		Accepted: 1007

Description

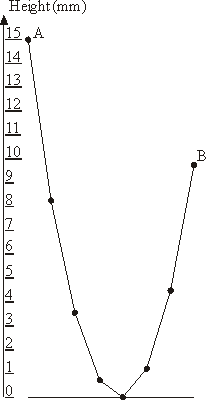The New Year garland consists of N lamps attached to a common wire that hangs down on the ends to which outermost lamps are affixed. The wire sags under the weight of lamp in a particular way: each lamp is hanging at the height that is 1 millimeter lower than the average height of the two adjacent lamps.

The leftmost lamp in hanging at the height of A millimeters above the ground. You have to determine the lowest height B of the rightmost lamp so that no lamp in the garland lies on the ground though some of them may touch the ground.

You shall neglect the lamp's size in this problem. By numbering the lamps with integers from 1 to N and denoting the ith lamp height in millimeters as Hi we derive the following equations:

H1 = A 
Hi = (H_i-1 + H_i+1)/2 - 1, for all 1 < i < N 
HN = B 
Hi >= 0, for all 1 <= i <= N

The sample garland with 8 lamps that is shown on the picture has A = 15 and B = 9.75.

Input

The input file consists of a single line with two numbers N and A separated by a space. N (3 <= N <= 1000) is an integer representing the number of lamps in the garland, A (10 <= A <= 1000) is a real number representing the height of the leftmost lamp above the ground in millimeters.

Output

Write to the output file the single real number B accurate to two digits to the right of the decimal point representing the lowest possible height of the rightmost lamp.

Sample Input

692 532.81

Sample Output

446113.34

Source

Northeastern Europe 2000

/*
* @Author: Lyucheng
* @Date:   2017-07-25 10:07:16
* @Last Modified by:   Lyucheng
* @Last Modified time: 2017-07-29 19:25:29
*/
/*
 题意：有一串项链，给出第一个珠子的位置，然后保证每个珠子不能掉到地上，也就是说高度必须大于等于零，让你求最后一个珠子的位置

 思路：二分答案就可以，判断条件可以推出公式
    H1=A
    H2=A/2 + H3/2 - 1
    H3=A/3 + (H4*2)/3 - 2
    ...
    Hn-1=A/(n-1) + (Hn*n-2)/n-1 - (n-2)
    然后逆向推过来

 错误：上面的公式可能存在损失精度的问题...可是打印了所有答案，真的没错...poj C++能过，但是G++就过不了

 改进：H[i] = 2 * H[i - 1] + 2 - H[i - 2];

 还有个问题，用printf输出就不行，用cout输出就可以
*/

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <iomanip>

#define MAXL -1
#define MAXR 1000+16
#define MAXN 1000+16
#define EXP 1e-9

using namespace std;

int n;
double A,B;
double F[MAXN];

bool ok(const double &x){
    F[]=x;
    for(int i=;i<=n;i++){
        F[i]=*F[i-]+-F[i-];
        if(F[i]<) return false;
    }
    B=F[n];
    return true;
}

int main(){
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    cin>>n>>A;
    F[]=A;
    double l=MAXL,r=MAXR,mid;
    for(int i=;i<;i++){
        mid=(l+r)/2.0;
        if(ok(mid)==true){
            r=mid;
        }else{
            l=mid;
        }
    }
    cout << fixed << setprecision() << B << endl;
    return ;
}