有关CUBLAS中的矩阵乘法函数

关于cuBLAS库中矩阵乘法相关的函数及其输入输出进行详细讨论。

▶ 涨姿势：

● cuBLAS中能用于运算矩阵乘法的函数有4个，分别是 cublasSgemm（单精度实数）、cublasDgemm（双精度实数）、cublasCgemm（单精度复数）、cublasZgemm（双精度复数），它们的定义（在 cublas_v2.h 和 cublas_api.h 中）如下。

 #define cublasSgemm cublasSgemm_v2
 CUBLASAPI cublasStatus_t CUBLASWINAPI cublasSgemm_v2
 (
     cublasHandle_t handle,
     cublasOperation_t transa, cublasOperation_t transb,
     int m, int n, int k,
     const float *alpha,
     const float *A, int lda,
     const float *B, int ldb,
     const float *beta,
     float *C, int ldc
 );

 #define cublasDgemm cublasDgemm_v2
 CUBLASAPI cublasStatus_t CUBLASWINAPI cublasDgemm_v2
 (
     cublasHandle_t handle,
     cublasOperation_t transa, cublasOperation_t transb,
     int m, int n, int k,
     const double *alpha,
     const double *A, int lda,
     const double *B, int ldb,
     const double *beta,
     double *C, int ldc
 );

 #define cublasCgemm cublasCgemm_v2
 CUBLASAPI cublasStatus_t CUBLASWINAPI cublasCgemm_v2
 (
     cublasHandle_t handle,
     cublasOperation_t transa, cublasOperation_t transb,
     int m, int n, int k,
     const cuComplex *alpha,
     const cuComplex *A, int lda,
     const cuComplex *B, int ldb,
     const cuComplex *beta,
     cuComplex *C, int ldc
 );

 #define cublasZgemm cublasZgemm_v2
 CUBLASAPI cublasStatus_t CUBLASWINAPI cublasZgemm_v2
 (
     cublasHandle_t handle,
     cublasOperation_t transa, cublasOperation_t transb,
     int m, int n, int k,
     const cuDoubleComplex *alpha,
     const cuDoubleComplex *A, int lda,
     const cuDoubleComplex *B, int ldb,
     const cuDoubleComplex *beta,
     cuDoubleComplex *C,
     int ldc
 );

● 四个函数形式相似，均输入了14个参数。该函数实际上是用于计算 C = α A B +β C 的，其中 A_m×k 、B_k×n 、C_m×n 为矩阵，α 、β 为标量。每个参数的意义如下，过后逐一详细说明

　　 cublasHandle_t handle         调用 cuBLAS 库时的句柄

　　 cublasOperation_t transa    是否转置矩阵A

　　 cublasOperation_t transb    是否转置矩阵B

　　int m                                     矩阵A的行数，等于矩阵C的行数

　　 int n                                     矩阵B的列数，等于矩阵C的列数

　　 int k                                     矩阵A的列数，等于矩阵B的行数

　　 const float *alpha              标量 α 的指针，可以是主机指针或设备指针，只需要计算矩阵乘法时命 α = 1.0f

　　 const float *A                     矩阵（数组）A 的指针，必须是设备指针

　　 int lda                                 矩阵 A 的主维（leading dimension）

　　 const float *B                     矩阵（数组）B 的指针，必须是设备指针

　　 int ldb                                 矩阵 B 的主维

　　 const float *beta               标量 β 的指针，可以是主机指针或设备指针，只需要计算矩阵乘法时命 β = 0.0f

　　 float *C 　　　                   矩阵（数组）C 的指针，必须是设备指针

　　 int ldc  　　　                    矩阵 C 的主维　　　　　　　　　

　　测试用例如下（完整的代码在本文末尾），其中维度 m = 2, n = 4, k = 3。

　　　

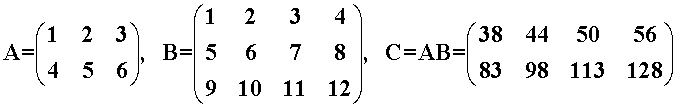
①  cublasDataType_t handle

　　一个有关cuBLAS库的上下文的句柄，之后需要传递给API函数，即计算乘法的函数。在随笔 http://www.cnblogs.com/cuancuancuanhao/p/7760562.html 中给出了这个句柄的使用方法，简单说就是以下过程。

 ...// 准备 A, B, C 以及使用的线程网格、线程块的尺寸

 // 创建句柄
 cublasHandle_t handle;
 cublasCreate(&handle);

 // 调用计算函数
 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, &alpha, *B, n, *A, k, &beta, *C, n);

 // 销毁句柄
 cublasDestroy(handle);

 ...// 回收计算结果，顺序可以和销毁句柄交换

　　另外，创建句柄的函数 cublasCreate() 会返回一个 cublasStatus_t 类型的值，用来判断句柄是否创建成功，该值在 cublas_api.h 中定义如下，可见只有其等于0的时候才能认为创建成功。

 typedef enum{
     CUBLAS_STATUS_SUCCESS         =,
     CUBLAS_STATUS_NOT_INITIALIZED =,
     CUBLAS_STATUS_ALLOC_FAILED    =,
     CUBLAS_STATUS_INVALID_VALUE   =,
     CUBLAS_STATUS_ARCH_MISMATCH   =,
     CUBLAS_STATUS_MAPPING_ERROR   =,
     CUBLAS_STATUS_EXECUTION_FAILED=,
     CUBLAS_STATUS_INTERNAL_ERROR  =,
     CUBLAS_STATUS_NOT_SUPPORTED   =,
     CUBLAS_STATUS_LICENSE_ERROR   =
 } cublasStatus_t;

②  cublasOperation_t transa, cublasOperation_t transb

　　两个“是否需要对输入矩阵 A、B 进行转置”的参数，cuBLAS 库难点之一。简单地说，cuBLAS 中关于矩阵的存储方式与 fortran、MATLAB 类似，是列优先，而非 C / C++ 中的行优先。

　　

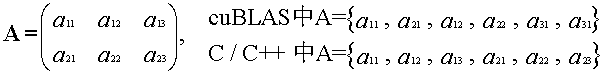
　　当把 C / C++ 中行优先保存的二维数组 A 以一维形式输入 cuBLAS 时，会被 cuBLAS 理解为列优先存储。这时如果保持 A 的行、列数不变，则矩阵 A 会发生重排（过程类似 MATLAB 中的 reshape(A, [size(A,2), size(A, 1)])），除非同时交换 A 的行、列数，此时结果才恰好等于 A 的转置，在一般的调用过程中正是利用了这一条性质。于是 cuBLAS 事先利用这个参数询问，是否需要将矩阵 A、B 进行转置。在这里，我尝试了大量的例子来说明 cuBLAS 中对数组的操作。

　　该参数表示的转置有三种，CUBLAS_OP_N（不转置），CUBLAS_OP_T（普通转置），CUBLAS_OP_C（共轭转置）。例子中仅涉及单精度实数运算，采用 CUBLAS_OP_N 或者 CUBLAS_OP_T 。

 typedef enum {
     CUBLAS_OP_N = ,
     CUBLAS_OP_T = ,
     CUBLAS_OP_C =
 } cublasOperation_t;

　　

　　1° （错误示范）直接将A、B放入函数中，转置参数均取为 CUBLAS_OP_N（lda、ldb、ldc 正常地取作各矩阵的行数，后面会解释其作用，到时候再回过头来看就好）。

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, &alpha, *A, m, *B, k, &beta, *C, m);

　　过程和结果如下。cuBLAS 自动将输入的 A、B 理解为列优先存储，而且保持 A、B 的行、列数保持不变，即将其当作 A₁ 和 B₁（注意这里 A₁、B₁ 并不等于 A、B 的转置）。计算乘积 C₁ 作为输出，最后主机将输出 C₁ 当成是行优先的矩阵，就成了 C₂ 的模样。显然这样计算的结果显然不是我们期望的 C 。（图中的“列优先”和“行优先”分别代表进入和退出 cuBLAS 时发生的强制转化，不要理解为其他意思）

　　

　　2° （正确过程）这一般教程上的调用过程。利用了性质 A B = (B^T A^T)^T。我们把一个行优先的矩阵看作列优先的同时，交换其行、列数，其结果等价于得到该矩阵的转置，列优先转行优先的原理相同。所以我们可以在调用该函数的时候，先放入 B 并交换参数 k 和 n 的位置，再放入 A 并交换参数 m 和 k 的位置，这样就顺理成章得到了结果的 C （所有转换由cuBLAS完成，不需要手工调整数组），注意以下调用语句中红色的部分。

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, n, m, k, &alpha, *B, n, *A, k, &beta, *C, n);

　　过程和结果如下。cuBLAS读取 B 和 A 的时候虽然进行了重排，但是

　　

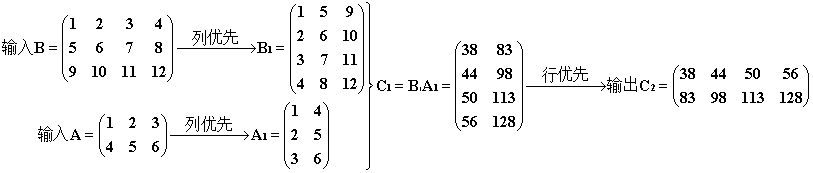
　　2.5° （尝试手工转置，为 3° 作铺垫）如果我们并不想运用 2° 中的奇技淫巧，而是希望按顺序将 A、B 输入 cuBLAS 中运算。我们可以先尝试手工将 A、B 转化为列优先存，储然后再调用该函数，最后将输出的 C 转化回行优先即可。转化过程如下：

 // 行优先转列优先，只改变存储方式，不改变矩阵尺寸
 void rToC(float *a, int ha, int wa)// 输入数组及其行数、列数
 {
     int i;
     float *temp = (float *)malloc(sizeof(float) * ha * wa);// 存放列优先存储的临时数组

     for (i = ; i < ha * wa; i++)         // 找出列优先的第 i 个位置对应行优先坐标进行赋值
         temp[i] = a[i / ha + i % ha * wa];
     for (i = ; i < ha * wa; i++)         // 覆盖原数组
         a[i] = temp[i];
     free(temp);
     return;
 }

 // 列优先转行优先
 void cToR(float *a, int ha, int wa)
 {
     int i;
     float *temp = (float *)malloc(sizeof(float) * ha * wa); 

     for (i = ; i < ha * wa; i++)         // 找出行优先的第 i 个位置对应列优先坐标进行赋值
         temp[i] = a[i / wa + i % wa * ha];
     for (i = ; i < ha * wa; i++)
         a[i] = temp[i];
     free(temp);
     return;
 }

　　这样一来，我们的调用过程如下（跟 1° 中参数位置一模一样）注意上面的转换函数中我没有交换矩阵 a 的行数、列数，所以在下面的调用中仍然有 m = 2, n = 4, k = 3。

 rToC(h_A, m, k);
 rToC(h_B, k, n);

 ...// 准备工作

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, &alpha, d_A, m, d_B, k, &beta, d_C, m);

 ...// 回收工作        

 cToR(h_CUBLAS, m, n);

　　过程和结果如下。注意经过 rToC处理得到的矩阵，以 A₁为例，它相当于用列优先的方式（竖着走）把 A 遍历得到的轨迹按行优先的方式存放（横着放）。可见矩阵 A、B、C 一波三折，但是最终获得了我们期望的结果。

　　

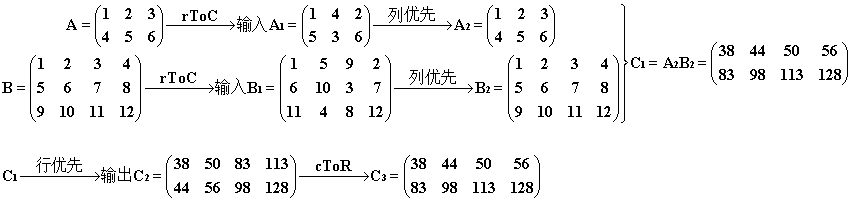
　　3° （使用 cuBLAS 自动转置）有了2.5° 的基础，我们就很好理解参数 cublasOperation_t transa, cublasOperation_t transb 的作用了。这两个参数就是在问，是否要在 cuBLAS 内部完成上面的 rToC过程。如果我们选择参数 CUBLAS_OP_T，那么不再需要手动地将 A、B 进行转换（但是仍需要对输出 C 进行转换），直接上代码

 cublasSgemm(handle, CUBLAS_OP_T, CUBLAS_OP_T, m, n, k, &alpha, d_A, k, d_B, n, &beta, d_C, m);

 ...// 回收工作

 cToR(h_CUBLAS, matrix_size.uiHC, matrix_size.uiWC);

　　过程和结果如下。我们发现主维数 lda、ldb 已经用上了，它们分别等于 A₂、B₂ 的行数（在列优先存储中矩阵的行数是维度的第一个分量，故称主维）。其实图中可以省略 “→ A₂” 这一中间步骤，但是为了突出“转置”的意味，我们把它画出来，再经过CUBLAS_OP_T 处理，方便理解。最终我们获得了期望的结果 C₃ ，我们发现这种方式省去了对 A、B 的 rToC 操作，但是 C₂ 的 cToR 操作还是逃不掉，没有 2° 来的巧妙。

　　

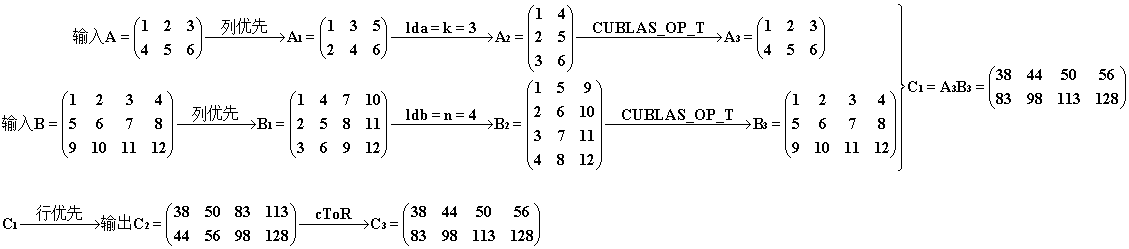
　　4° 有了以上的说明，我们就可以对A、B的不同情况再加以利用，得到下面两种组合，他们都能得到正确的结果。过程图示就是 2.5° 和 3° 的图进行组合，其余不变。

 // A转B不转
 //rToC(h_A, matrix_size.uiHA,matrix_size.uiWA);
 rToC(h_B, matrix_size.uiHB, matrix_size.uiWB);

 ...

 cublasSgemm(handle, CUBLAS_OP_T, CUBLAS_OP_N, m, n, k, &alpha, d_A, k, d_B, k, &beta, d_C, m);

 ...

 cToR(h_CUBLAS, matrix_size.uiHC, matrix_size.uiWC);

 // B转A不转
 rToC(h_A, matrix_size.uiHA,matrix_size.uiWA);
 //rToC(h_B, matrix_size.uiHB, matrix_size.uiWB);

 ...

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_T, m, n, k, &alpha, d_A, m, d_B, n, &beta, d_C, m);

 ...

 cToR(h_CUBLAS, matrix_size.uiHC, matrix_size.uiWC);

③  int lda, int ldb, int ldc

　　主维（leading dimension）。如果我们想要计算 A_m×k B_k×n = C_m×n，那 m、n、k 三个参数已经固定了所有尺寸，为什么还要一组主维参数呢？看完了上面部分我们发现，输入的矩阵 A、B 在整个计算过程中会发生变形，包括行列优先变换和转置变换，所以需要一组参数告诉该函数，矩阵变形后应该具有什么样的尺寸。参考 CUDA 的教程 CUDA Toolkit Documentation v9.0.176，对这几个参数的说明比较到位。

　　当参数 transa 为 CUBLAS_OP_N 时，矩阵 A 在 cuBLAS 中的尺寸实际为 lda × k，此时要求 lda ≥ max(1, m)（否则由该函数直接报错，输出全零的结果）；当参数 transa 为 CUBLAS_OP_T 或 CUBLAS_OP_C 时，矩阵 A 在 cuBLAS 中的尺寸实际为 lda × m，此时要求 lda ≥ max(1, k) 。

　　transb 为 CUBLAS_OP_N 时，B 尺寸为 ldb × n，要求 ldb ≥ max(1, k)； transb 为 CUBLAS_OP_T 或 CUBLAS_OP_C 时，B尺寸为 ldb × k，此时要求 ldb ≥ max(1, n) 。

　　C 尺寸为 ldc × n，要求 ldc ≥ max(1, m)。

　　可见，是否需要该函数帮我们转置矩阵 A 会影响 A 在函数中的存储。而主维正是在这一过程中起作用。特别地，如果按照一般教程中的方法来调用该函数，三个主维参数是不用特别处理的。

　　上面的教程中只要求了三个主维参数的下界，为此，我尝试调高三个参数，获得了一些有启发性的结果。

　　Ⅰ.ldb + 1

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, n, m, k, &alpha, d_B, n + 1, d_A, k, &beta, d_C, n);

　　结果和过程。注意 B₁ 中多出来的部分被用零来填充了，计算 C₁ 的时候是依其尺寸来进行的，若 C₁ 的尺寸上没有加 1，则最后一行不进行计算。

　　

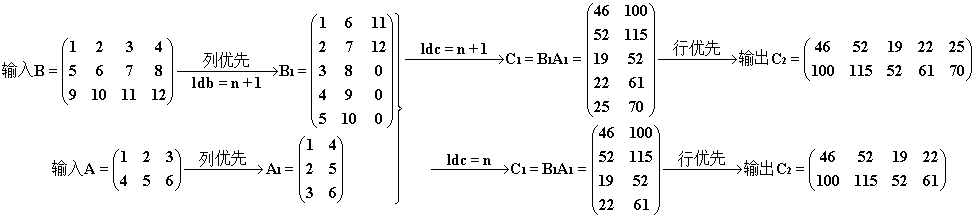
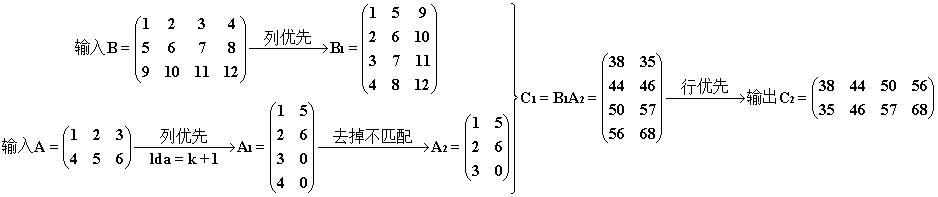
　　Ⅱ. lda + 1

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, n, m, k, &alpha, d_B, n, d_A, k + , &beta, d_C, n);

　　结果和过程。注意 A₁ 在参与乘法时去掉了多出的行（其实应该是计算乘法时行程长 = min (B₁ 列数，A₁ 行数) = 3）。

　　

　　Ⅲ. ldc + 1

 cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, n, m, k, &alpha, d_B, n, d_A, k, &beta, d_C, n + );

　　结果和过程。注意计算出来的 C₁ 自动补充了零行，但是在输出的时候连着零一起输出，并且把最后的两个元素挤掉了。

　　

▶ 测试用源代码：

 #include <assert.h>
 #include <helper_string.h>
 #include <cuda_runtime.h>
 #include <cublas_v2.h>
 #include <helper_functions.h>
 #include <helper_cuda.h>

 // 存放各矩阵维数的结构体
 typedef struct
 {
     unsigned int wa, ha, wb, hb, wc, hc;
 } matrixSize;

 // 行优先转列优先，只改变存储方式，不改变矩阵尺寸
 void rToC(float *a, int ha, int wa)
 {
     int i;
     float *temp = (float *)malloc(sizeof(float) * ha * wa);// 存放列优先存储的临时数组

     for (i = ; i < ha * wa; i++)         // 找出列优先的第 i 个位置对应行优先位置进行赋值
         temp[i] = a[i / ha + i % ha * wa];
     for (i = ; i < ha * wa; i++)         // 覆盖原数组
         a[i] = temp[i];
     free(temp);
     return;
 }

 // 列优先转行优先
 void cToR(float *a, int ha, int wa)
 {
     int i;
     float *temp = (float *)malloc(sizeof(float) * ha * wa); 

     for (i = ; i < ha * wa; i++)         // 找出列优先的第 i 个位置对应行优先位置进行赋值
         temp[i] = a[i / wa + i % wa * ha];
     for (i = ; i < ha * wa; i++)
         a[i] = temp[i];
     free(temp);
     return;
 }

 // 计算矩阵乘法部分
 int matrixMultiply()
 {
     matrixSize ms;
     ms.wa = ;
     ms.ha = ;
     ms.wb = ;
     ms.hb = ms.wa;
     ms.wc = ms.wb;
     ms.hc = ms.ha;

     unsigned int size_A = ms.wa * ms.ha;
     unsigned int mem_size_A = sizeof(float) * size_A;
     float *h_A = (float *)malloc(mem_size_A);
     unsigned int size_B = ms.wb * ms.hb;
     unsigned int mem_size_B = sizeof(float) * size_B;
     float *h_B = (float *)malloc(mem_size_B);

     for (int i = ; i < ms.ha*ms.wa; i++)
         h_A[i] = i + ;
     for (int i = ; i < ms.hb*ms.wb; i++)
         h_B[i] = i + ;

     // 转换函数，按需取用
     //rToC(h_A, ms.ha,ms.wa);
     //rToC(h_B, ms.hb, ms.wb);

     float *d_A, *d_B, *d_C;
     unsigned int size_C = ms.wc * ms.hc;
     unsigned int mem_size_C = sizeof(float) * size_C;
     float *h_CUBLAS = (float *) malloc(mem_size_C);
     cudaMalloc((void **) &d_A, mem_size_A);
     cudaMalloc((void **) &d_B, mem_size_B);
     cudaMemcpy(d_A, h_A, mem_size_A, cudaMemcpyHostToDevice);
     cudaMemcpy(d_B, h_B, mem_size_B, cudaMemcpyHostToDevice);
     cudaMalloc((void **) &d_C, mem_size_C);

     dim3 threads(,);
     dim3 grid(,);

     //cuBLAS代码
     const float alpha = 1.0f;
     const float beta  = 0.0f;
     int m = ms.ha, n = ms.wb, k = ms.wa;

     cublasHandle_t handle;
     cublasCreate(&handle);

     cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, n, m, k, &alpha, d_B, n, d_A, k, &beta, d_C, n);

     cublasDestroy(handle);

     cudaMemcpy(h_CUBLAS, d_C, mem_size_C, cudaMemcpyDeviceToHost);

     // 转换函数，按需取用
     //cToR(h_CUBLAS, ms.hc, ms.wc);

     printf("\nResult C=\n");
     for (int i = ; i < ms.hc*ms.wc; i++)
     {
         printf("%3.2f\t", h_CUBLAS[i]);
         if ((i + ) % ms.wc == )
             printf("\n");
     }

     free(h_A);
     free(h_B);
     free(h_CUBLAS);
     cudaFree(d_A);
     cudaFree(d_B);
     cudaFree(d_C);
     return ;
 }

 int main()
 {
     matrixMultiply();
     getchar();
     return ;
 }

▶ 输出结果：

Result C=
38.00   44.00   50.00   56.00
83.00   98.00   113.00  128.00

▶ 补充

● 挂一个傻[哔—]，今天才看到的，注意发布时间：https://blog.csdn.net/sinat_24143931/article/details/79487357