HDU2973（威尔逊定理）

YAPTCHA

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 875    Accepted Submission(s): 458

Problem Description

The math department has been having problems lately. Due to immense amount of unsolicited automated programs which were crawling across their pages, they decided to put Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart
on their webpages. In short, to get access to their scientific papers, one have to prove yourself eligible and worthy, i.e. solve a mathematic riddle.





However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).



The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute




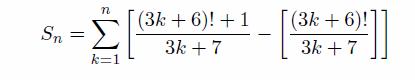
where [x] denotes the largest integer not greater than x.

 

Input

The first line contains the number of queries t (t <= 10^6). Each query consist of one natural number n (1 <= n <= 10^6).

 

Output

For each n given in the input output the value of Sn.

 

Sample Input

13
1
2
3
4
5
6
7
8
9
10
100
1000
10000

 

Sample Output

0
1
1
2
2
2
2
3
3
4
28
207
1609

 

Source

Central European Programming Contest 2008

威尔逊定理：当( p -1 )! ≡ -1 ( mod p ) 时，p为素数。

证明如下

充分性：

当p不是素数，那么令p=a*b ，其中1 < a < p-1 ,1 < b < p-1.

(1)若a≠b,

因为(p-1)!=1*2*...*a*...*b*...*p-1,

所以(p-1)!≡ 0 (mod a)

(p-1)!≡ 0 (mod b)

可得(p-1)!≡ 0 (mod a*b) ，

即 (p-1)!≡ 0 (mod p)

与( p -1 )! ≡ -1 ( mod p )  矛盾

(2)若a=b

因为(p-1)!=1*2*...*a*...*2a*...*p-1.

所以(p-1)!≡ 0 (mod a)

(p-1)!≡ 0 (mod 2a)

可得(p-1)!≡ 0 (mod a*2a) => (p-1)!≡ 0 (mod a*a) ，

即 (p-1)!≡ 0 (mod p)

与( p -1 )! ≡ -1 ( mod p )  矛盾

因此p只能是素数。

必要性：

当p为2，( p -1 )! ≡ -1 ( mod p ) 显然成立

当p为3，( p -1 )! ≡ -1 ( mod p ) 显然成立

对于p>=5，令M={2,3,4,...,p-2}.

对于a∈M，令N={a,2*a,3*a,4*a,....(p-2)*a,(p-1)*a}

令1 <= t1 <= p-1 ,1 <= t2 <= p-1,t1 ≠ t2

那么t1*a∈N，t2*a∈N。

若t1*a≡t2*a (mod p) ，那么|t1-t2|*a ≡ 0 (mod p)。

因为|t1-t2|*a∈N，与N中元素不能被p除尽矛盾。

所以t1*a≡t2*a不成立。

那么N中元素对p取模后形成的集合为{1,2,3,4,...,p-1}.

设x*a ≡ 1 (mod p)。

当x=1时， x*a=a, 对p取模不为1，所以不成立。

当x=p-1时，(p-1)*a=p*a-a, 对p取模不为1，所以不成立。

当x=a时，a*a≡1 (mod p)，可得(a+1)*(a-1)≡ 0 (mod p),a=1或a=p-1 ，所以不成立。

综上所述，x,a∈M，并且当a不同时，x也随之不同。

所以，M集合中每一个元素a都能够找到一个与之配对的x，使得x*a ≡ 1 (mod p).

(p-1)!=1*2*3*...p-1

=1*(2*x1)*(3*x3)*...*(p-1)

所以， (p-1)!≡1*(p-1)    (mod p)

即，(p-1)!≡-1     (mod p)

证明完毕

#include <bits/stdc++.h>
using namespace std;

#define mem(a) memset(a, 0, sizeof(a))
const int maxn = 1e6+100;
int ans[maxn*3+100];

int isprime(int n) {
	if (n == 1)	return 0;
	if (n == 2)	return 1;
	for (int i = 2; i*i<=n; i++) {
		if (n%i == 0)	return 0;
	}
	return 1;
}

void init() {
	mem(ans);
	for (int i = 1; i<maxn; i++) {
		if (isprime(i*3+7))	ans[i] = ans[i-1]+1;
		else	ans[i] = ans[i-1];
	}
}

int main() {
	init();
	int t;
	scanf("%d", &t);
	while (t --) {
		int n;
		scanf("%d", &n);
		printf("%d\n",ans[n]);
	}

	return 0;
}