ML笔记：Gradient Descent

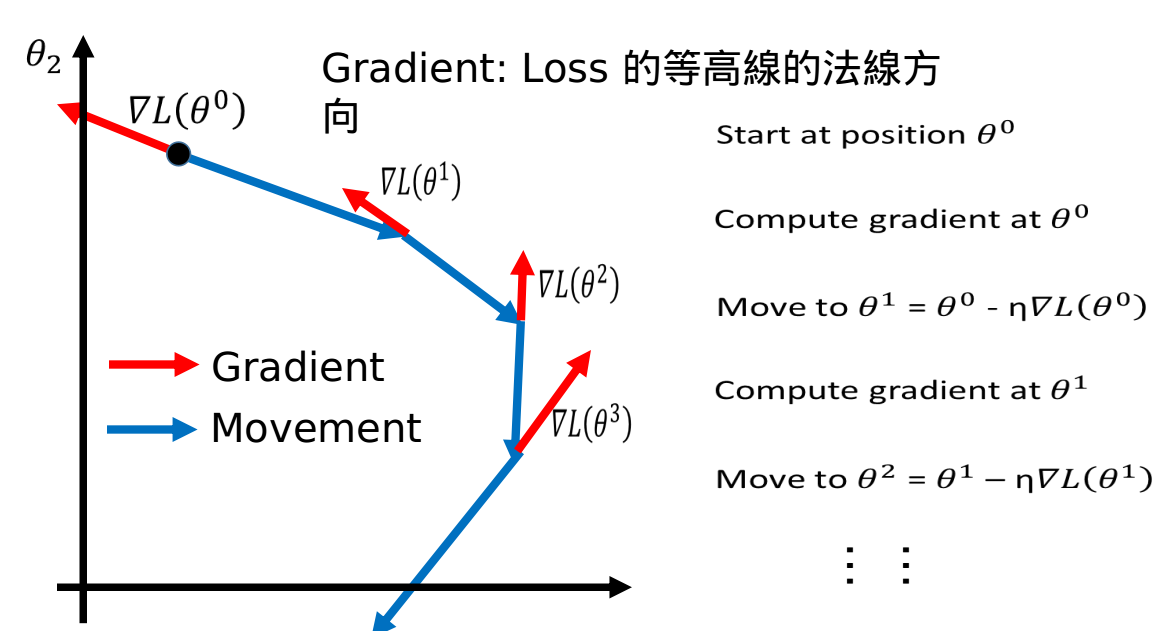
Review: Gradient Descent

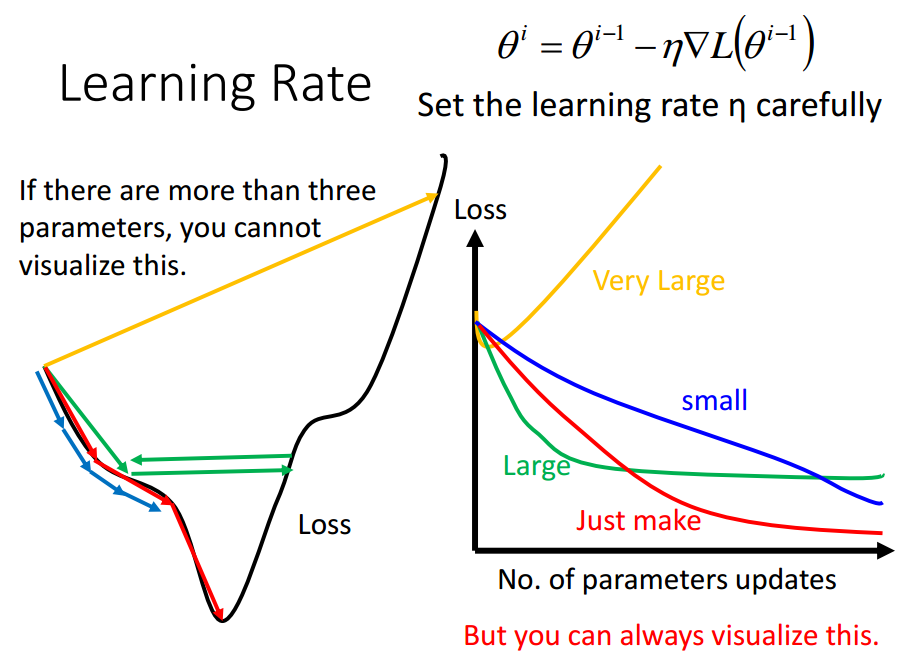
Tip 1: Tuning your learning rates

eta恰好,可以走到局部最小值点;

eta太小,走得太慢,也可以走到局部最小值点;

eta太大,很可能走不到局部最小值点,卡在某处上;

eta太太大,很可能走出去.

可以自动调节eta,

大原则是eta随更新次数的增长而减小,---time dependent

同时也要针对不同的参数设置不同的eta.---parameter dependent

有很多这样的自动调节eta的梯度下降方法,名称常以Ada开头,

其中较为简单的Adagrad:

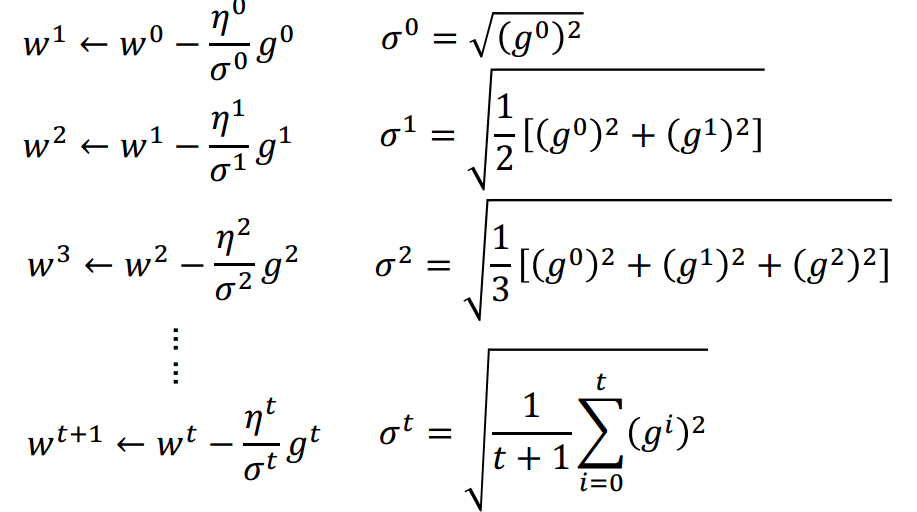
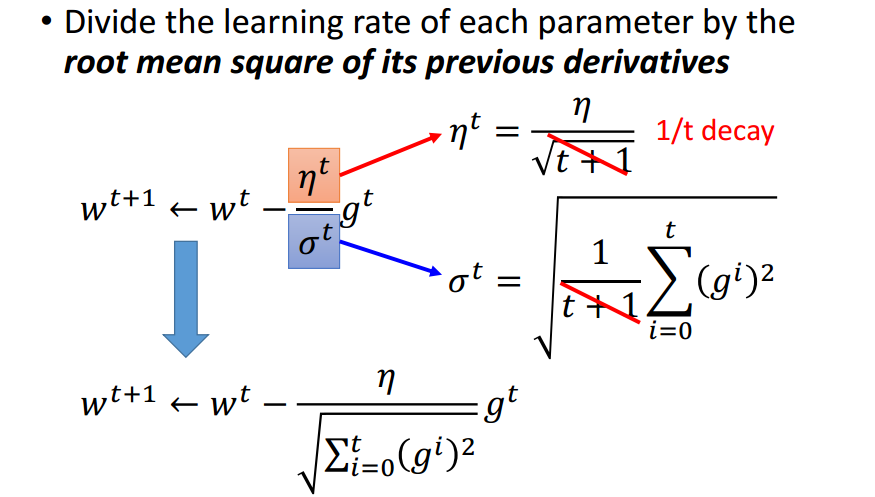
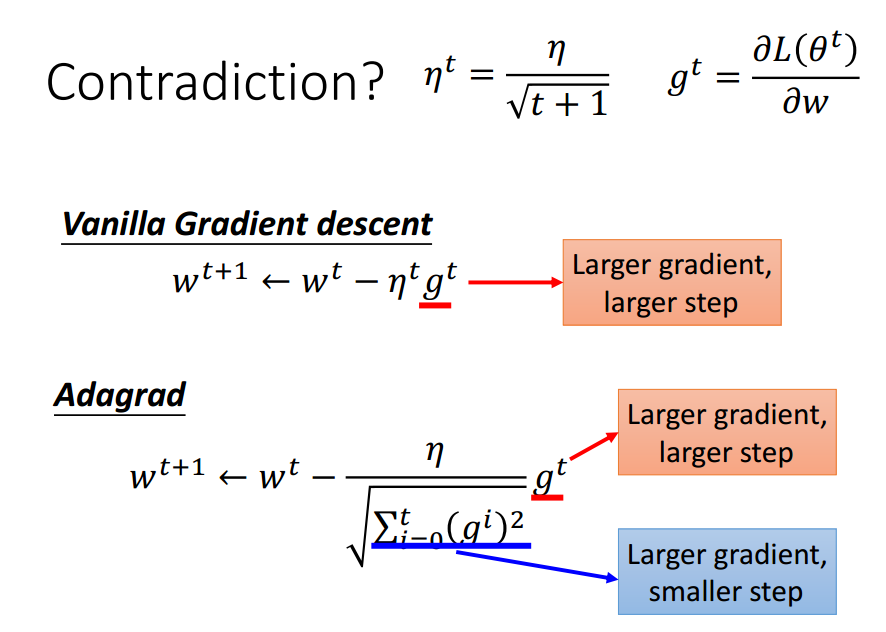
Adagrad强化反差.

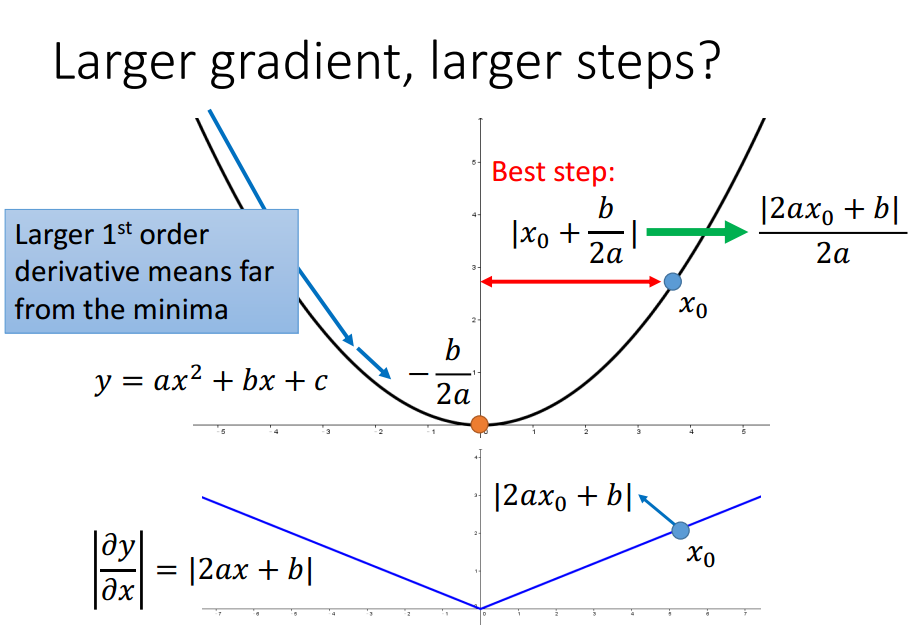
只考虑一个参数时,当前点与局部最优值点的距离与导数成正比,

考虑多个参数时,该结论不一定成立.

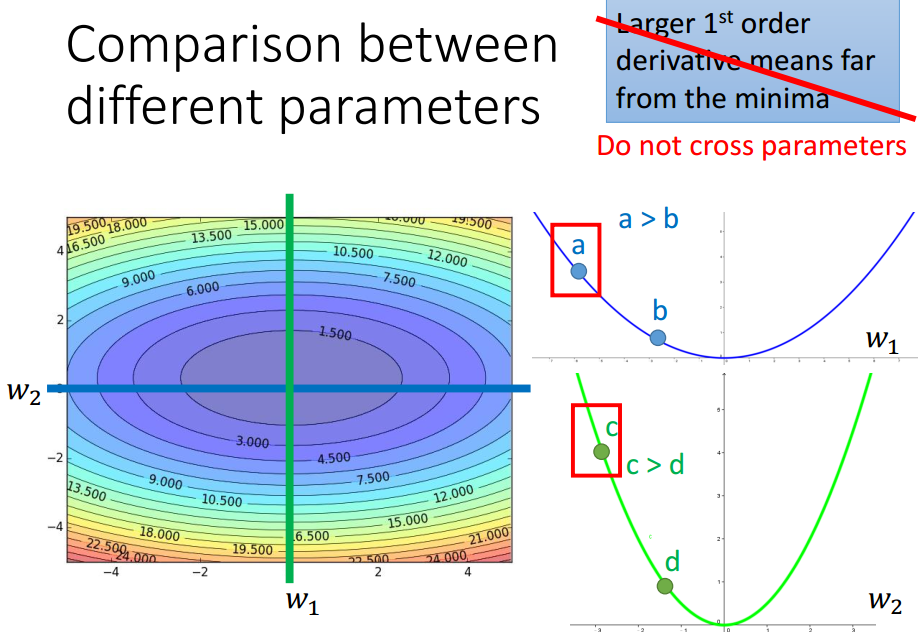
还需要考虑2阶导数来反映当前位置与局部最小值点的距离.

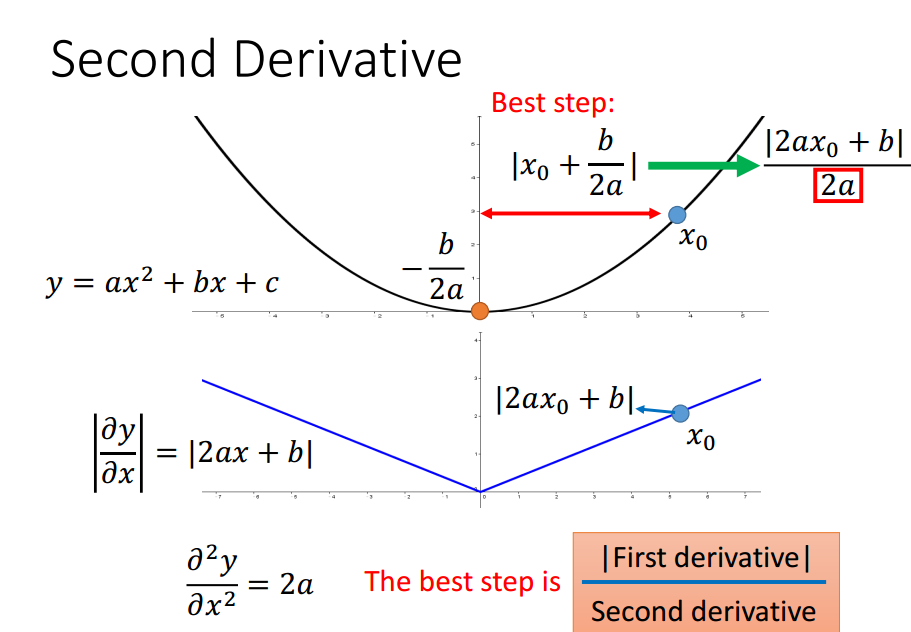
Adagrad的分母计算近似了2阶导数的计算.

没有增加额外的花费来估计2阶导数.

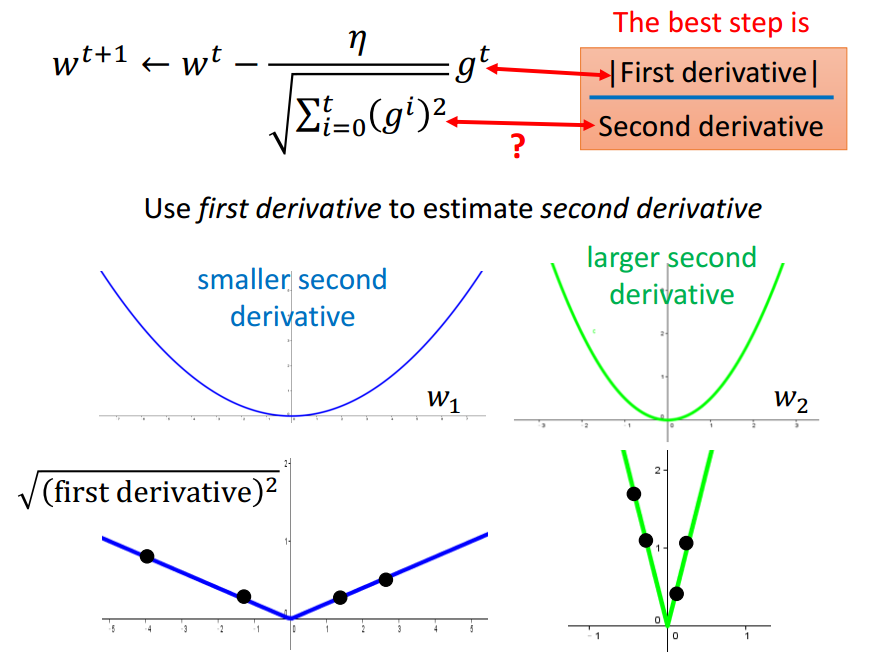
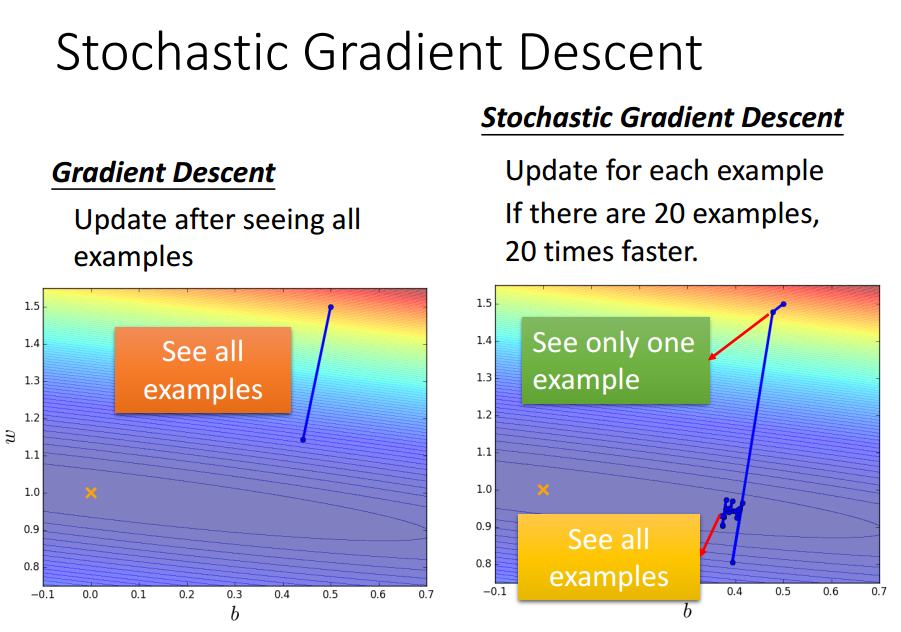
Tip 2: Stochastic Gradient Descent

梯度下降一次使用所有训练数据,

随机梯度下降一次使用单个训练数据.

SGD可能步伐小和散乱,但走得更快.

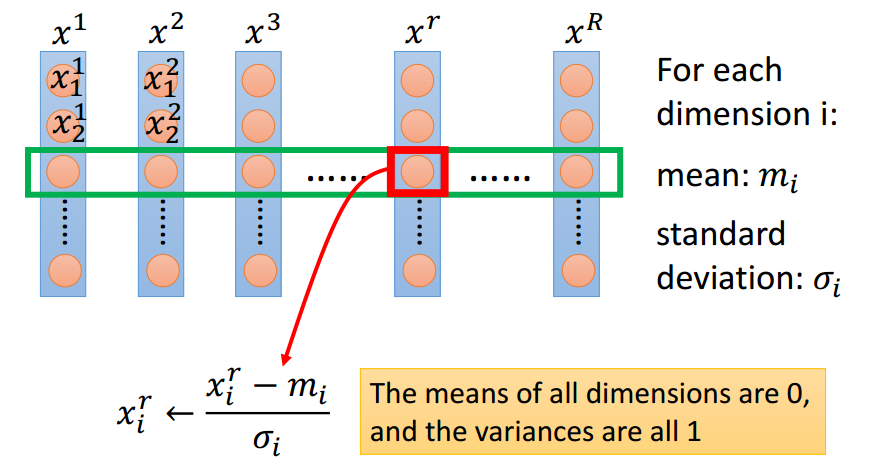
Tip 3: Feature Scaling

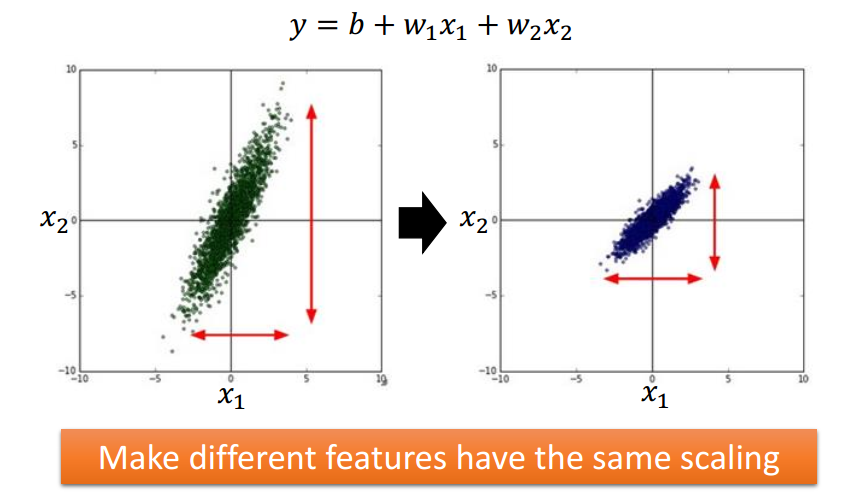
w1变化,y变化小;---w1对loss影响小

w2变化,y变化大.---w2对loss影响大

一般来说,椭圆形中不同方向的eta需求不一样,需要Ada梯度下降;

圆形中更新次数较少,因为无论椭圆形还是圆形,更新时都是沿着等高线的法线方向,

而圆形直接向着圆心走.

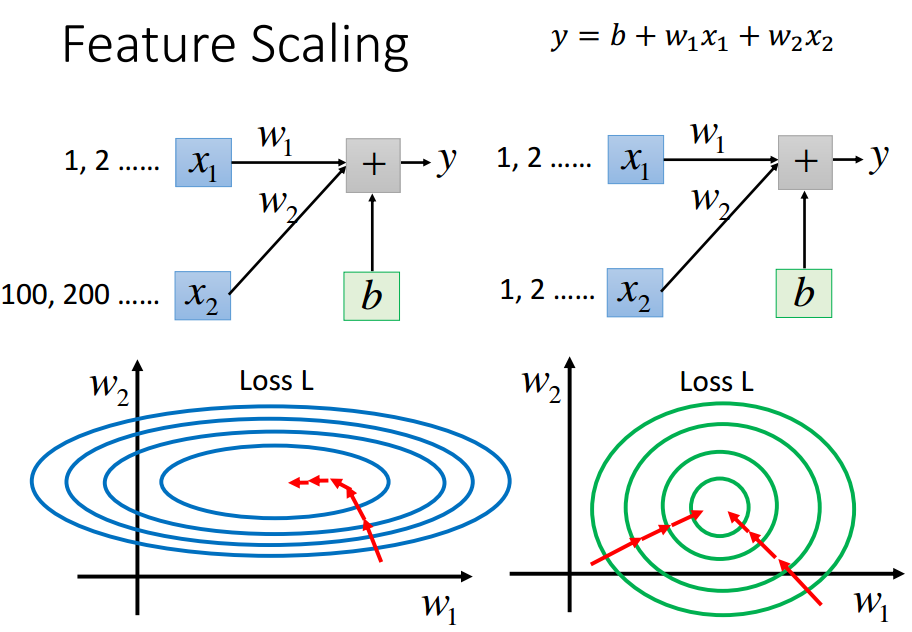
通过将特征归一化(均值0,方差1)实现特征缩放.

Theory

问题:

答案当然是不正确.

正式推导梯度下降能到达局部最小值点.

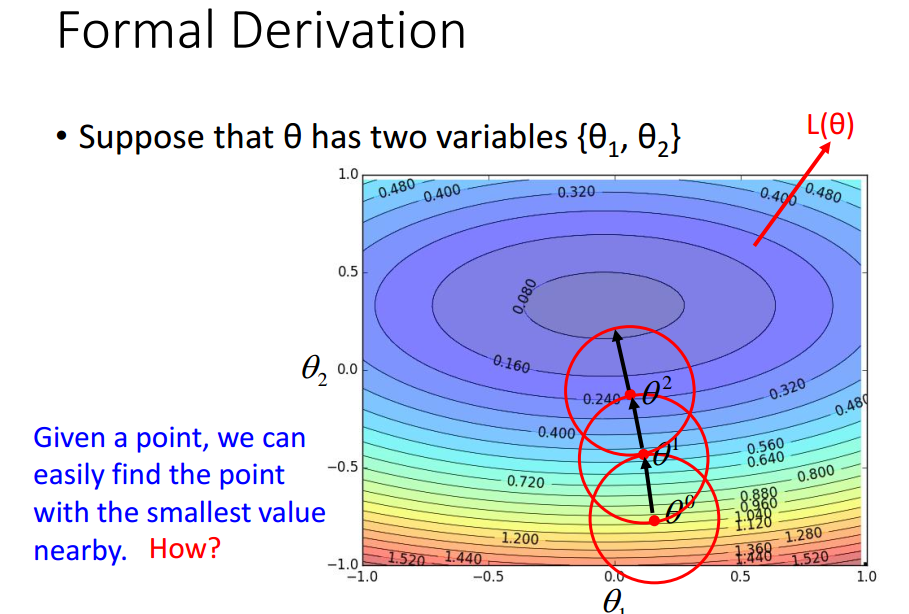
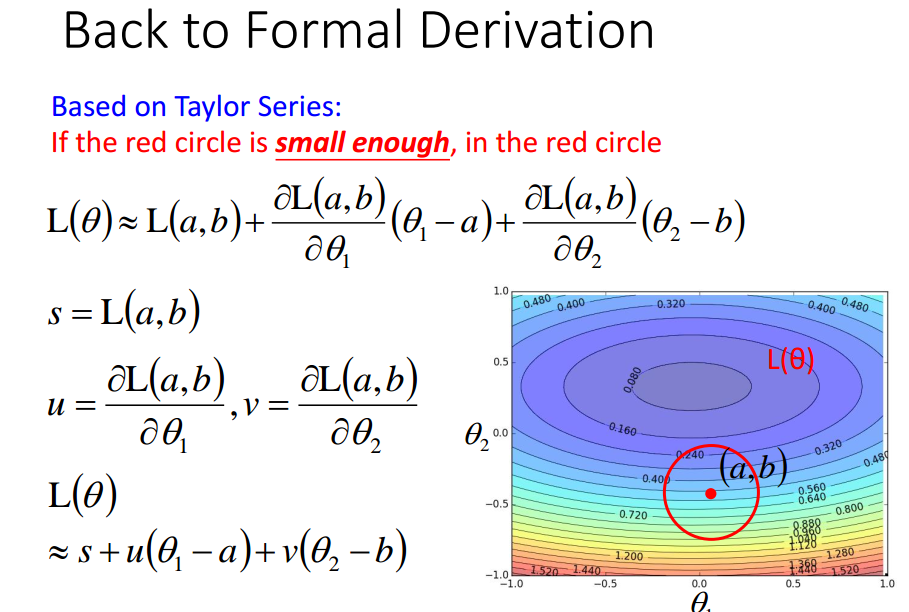
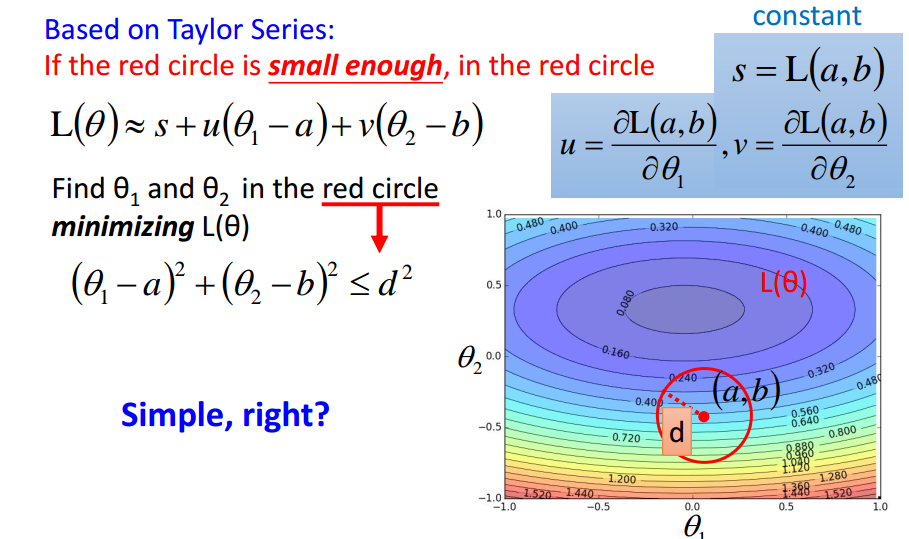
注意:

eta与红色半径成正比,

理论上,eta要充分小才能保证能到达局部最优值点,

实际上,eta只要小就行.

考虑泰勒二阶式的话,理论上eta值可以设得大点.---这种方式在deep learning中不见得那么普及

因为考虑二阶式会多出很多运算,deep learning中认为这样不划算.

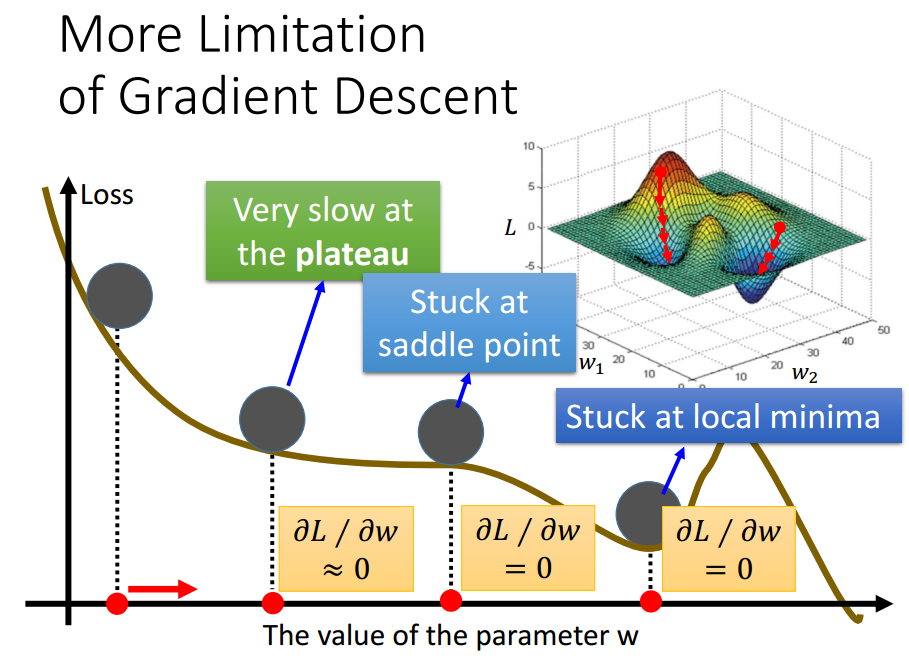
Limitation

实际操作中,很少情况下导数会exactly为0.

所以,真正问题是,该点实际在高原处,但导数小于阈值,

停下,但此时离局部最优值点还很远.