线性代数-矩阵-【5】矩阵化简 C和C++实现

点击这里可以跳转至

【1】矩阵汇总：http://www.cnblogs.com/HongYi-Liang/p/7287369.html

【2】矩阵生成：http://www.cnblogs.com/HongYi-Liang/p/7275278.html

【3】矩阵加减：http://www.cnblogs.com/HongYi-Liang/p/7287403.html

【4】矩阵点乘：http://www.cnblogs.com/HongYi-Liang/p/7287324.html

【5】矩阵化简：现在的位置

（待续）

...

---

C++语言：

高斯消元法：

继续使用这个矩阵

当我们使用高斯消元（无回代）化简这个矩阵，是这样算的：

上述过程归纳为：

1. 找到第一行行的主元（第一行第一个数：1）
2. 消除第而三行的的第一个数（r2-2*r1;r3-4*r1）
3. 找到第二行的主元（第二行第二个数：-2）
4. 消除第三行的第二个数（r3-3/2*r2）

可以发现实际上是1和2两个步骤的循环，所以写成循环的形式

• 从第一行开始到最后一行

1. 找主元：找出第i的主元(第i行第i个数)
2. 消元：消除下面所有行的第i个数（下面每一行减去x倍的第一行来消除第i列）

到目前为止，基本达到消元的目的了，但是有一些小小的瑕疵

我们可能碰到一个这样矩阵，有一行全是0,例如这个：

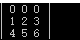
那么我们在步骤1中搜索到主元为0的话，0的任意倍数都是0，会导致第2步无法进行。所以我们需要添加换行的操作，计算方法为：

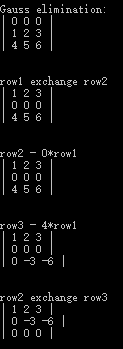
所以我们把代码逻辑修改成这样：

• 从第一行开始到最后一行

1. 找主元：找出第i的主元(第i行第i个数)，若主元为0，把第i行向下换行，直到找到有主元的行。若找不到主元，就开始找下一个
2. 消元：消除下面所有行的第i个数（下面每一行减去x倍的第一行来消除第i列）

下面就是高斯消元的主程序：

template <typename T>
bool Matrix<T>::GaussianElimination()
{
    Matrix<T> outputMatrix = *this;

    /*Gaussian elmiation*/
    for(int k=;k<outputMatrix.m_iRows;k++)
    {
        /*if all the pivot have been found*/
        if(k>=m_iColumns)
        {
            break;
        }

        /*exchange rows downward to find the row's pivot*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            /*pivot is non-zero*/
            if(outputMatrix.m_vecMatrix[k][k] != )
            {
                //T temp = outputMatrix.m_vecMatrix[0][0];
                break;
            }
            else
            {
                if(i < outputMatrix.m_iRows)
                {
                    outputMatrix.exchangeRows(k,i);
                }
            }
        }

        /*if there is no pivot in this row*/
        if(outputMatrix.m_vecMatrix[k][k] == )
        {
            break;
        }

        /*elimination:The rows below pivot row subtract times of pivot row*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows
            if(RowsfirstData != )
            {
                outputMatrix.m_vecMatrix[i][k]=;
                for(int j=k+;j<outputMatrix.m_iColumns;j++)
                {
                    outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;
                }
            }
        }
    }

    *this = outputMatrix;
    return true;
}

高斯-若尔当法

若尔当在高斯消元的基础上加上了回代过程，把矩阵化简成行最简式。我们在高斯消元的基础上加上和回代，方法跟高斯消元相反，用上面的行减下面的行，这里就不详细描述（展开查看代码）

rref()//化简矩阵成行最简

template <typename T>
bool Matrix<T>::rref()
{
    Matrix<T> outputMatrix = *this;
    int rank=;//the rank of the matrix, how many columns's pivot will it has(-1)

    /*Gaussian elmiation*/
    for(int k=;k<outputMatrix.m_iRows;k++)
    {
        /*if all the pivot elem have been found*/
        if(k>=m_iColumns)
        {
            break;
        }

        /*exchange rows downward to find the pivot row*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            /*pivot is non-zero*/
            if(outputMatrix.m_vecMatrix[k][k] != )
            {
                //T temp = outputMatrix.m_vecMatrix[0][0];
                rank++;
                break;
            }
            else
            {
                if(i < outputMatrix.m_iRows)
                {
                    outputMatrix.exchangeRows(k,i);
                }
            }
        }

        /*if there is no pivot in this row*/
        if(outputMatrix.m_vecMatrix[k][k] == )
        {
            break;
        }

        /*elimination:The rows below pivot row subtract times of pivot row*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows
            if(RowsfirstData != )
            {
                outputMatrix.m_vecMatrix[i][k]=;
                for(int j=k+;j<outputMatrix.m_iColumns;j++)
                {
                    outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;
                }
            }
        }
    }

    /*normalizing:set all pivots to 1*/
    for(int i=;i<outputMatrix.m_iRows;i++)
    {
        for(int j=;j<outputMatrix.m_iColumns;j++)
        {
            if(outputMatrix.m_vecMatrix[i][j] != )//pivot has been foound
            {
                double pivot = outputMatrix.m_vecMatrix[i][j];//get pivot
                for(int k=i;k<outputMatrix.m_iColumns;k++)
                {
                    outputMatrix.m_vecMatrix[i][k] /=pivot;
                }
                break;
            }
        }
    }

    /*Back substitution*/
    for(int i = rank;i>=;i--)
    {
        /*find a first non-zero elem (It is pivot)*/
        for(int j=;j<outputMatrix.m_iColumns;j++)
        {
            double times=;
            if(outputMatrix.m_vecMatrix[i][j] !=)//pivot found
            {
                for(int l=i-;l>=;l--)
                {
                    times = outputMatrix.m_vecMatrix[l][j]/outputMatrix.m_vecMatrix[i][j];
                    for(int k=j;k<outputMatrix.m_iColumns;k++)//tims of this row subtract by each columns in upon row
                    {
                        outputMatrix.m_vecMatrix[l][k] -= times*outputMatrix.m_vecMatrix[i][k];
                    }
                }
                break;
            }
        }
    }

    *this = outputMatrix;
    return true;
}

rrefmovie()//化简矩阵成行最简，并打印过程

template <typename T>
bool Matrix<T>::rrefmovie()
{
    Matrix<T> outputMatrix = *this;
    int rank=;//the rank of the matrix, how many columns's pivot will it has(-1)

    /*Gauss elmiation*/
    cout<<"Gauss elimination:"<<endl;
    outputMatrix.printfAll();
    for(int k=;k<outputMatrix.m_iRows;k++)
    {
        /*If all the pivot elem have been found*/
        if(k>=m_iColumns)
        {
            break;
        }

        /*Exchange rows downward to find the pivot row*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            /*Pivot is non-zero*/
            if(outputMatrix.m_vecMatrix[k][k] != )
            {
                rank++;
                break;
            }
            else
            {
                if(i < outputMatrix.m_iRows)
                {
                    outputMatrix.exchangeRows(k,i);
                }
            }
            if(k!=i)
            {
                cout<<"row"<<k+<<" exchange row"<<i+<<endl;//Debug
                outputMatrix.printfAll();
            }
        }

        /*If there is no pivot in this row*/
        if(outputMatrix.m_vecMatrix[k][k] == )
        {
            break;
        }

        /*Elimination:The rows below pivot row subtract times of pivot row*/
        for(int i=k+;i<outputMatrix.m_iRows;i++)
        {
            double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows
            if(RowsfirstData != )
            {
                outputMatrix.m_vecMatrix[i][k]=;
                for(int j=k+;j<outputMatrix.m_iColumns;j++)
                {
                    outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;
                }
            }
            cout<<"row"<<i+<<" - "<<RowsfirstData<<"*"<<"row"<<k+<<endl;//Debug
            outputMatrix.printfAll();
        }
    }

    /*Normalizing:set all rows pivot to 1*/
    for(int i=;i<outputMatrix.m_iRows;i++)
    {
        for(int j=;j<outputMatrix.m_iColumns;j++)
        {
            if(outputMatrix.m_vecMatrix[i][j] != )//pivot has been foound
            {
                double pivot = outputMatrix.m_vecMatrix[i][j];//get pivot
                for(int k=i;k<outputMatrix.m_iColumns;k++)
                {
                    outputMatrix.m_vecMatrix[i][k] /=pivot;
                }
                cout<<"row"<<i+<<" / "<<pivot<<endl;//Debug
                outputMatrix.printfAll();//Debug
                break;
            }
        }
    }

    /*Back substitution*/
    cout<<"Back substitution:"<<endl;
    for(int i = rank;i>=;i--)
    {
        /*find a first non-zero elem (It is pivot)*/
        for(int j=;j<outputMatrix.m_iColumns;j++)
        {
            double times=;
            if(outputMatrix.m_vecMatrix[i][j] !=)//pivot found
            {
                for(int l=i-;l>=;l--)
                {
                    times = outputMatrix.m_vecMatrix[l][j]/outputMatrix.m_vecMatrix[i][j];
                    for(int k=j;k<outputMatrix.m_iColumns;k++)//tims of this row subtract by each columns in upon row
                    {
                        outputMatrix.m_vecMatrix[l][k] -= times*outputMatrix.m_vecMatrix[i][k];
                    }
                    cout<<"row"<<l+<<" - "<<times<<"*"<<"row"<<i+<<endl;
                    outputMatrix.printfAll();
                }
                break;
            }
        }
    }

    *this = outputMatrix;
    return true;
}

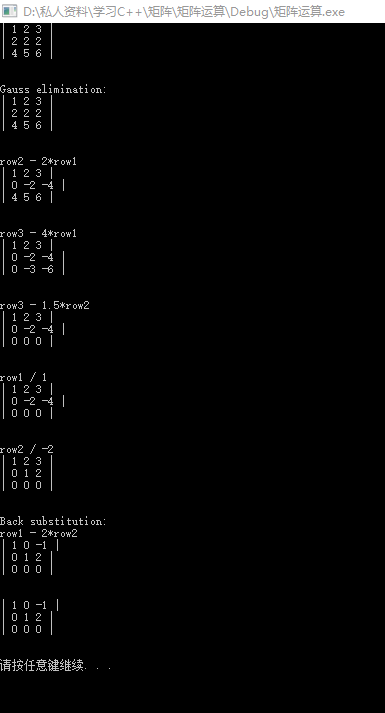
使用我们开始的矩阵测试：

    Matrix<double> matrix(,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.setSpecifiedElem(,,);
    matrix.printfAll();

    matrix.rrefmovie();
    matrix.printfAll();
    system("pause");

结果：