求最长公共子序列-DP问题

Longest common subsequence problem

The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from the longest common substring problem: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences.

Example

• LCS for input Sequences ABCDGH and AEDFHR is ADH of length 3.
• LCS for input Sequences AGGTAB and GXTXAYB is GTAB of length 4

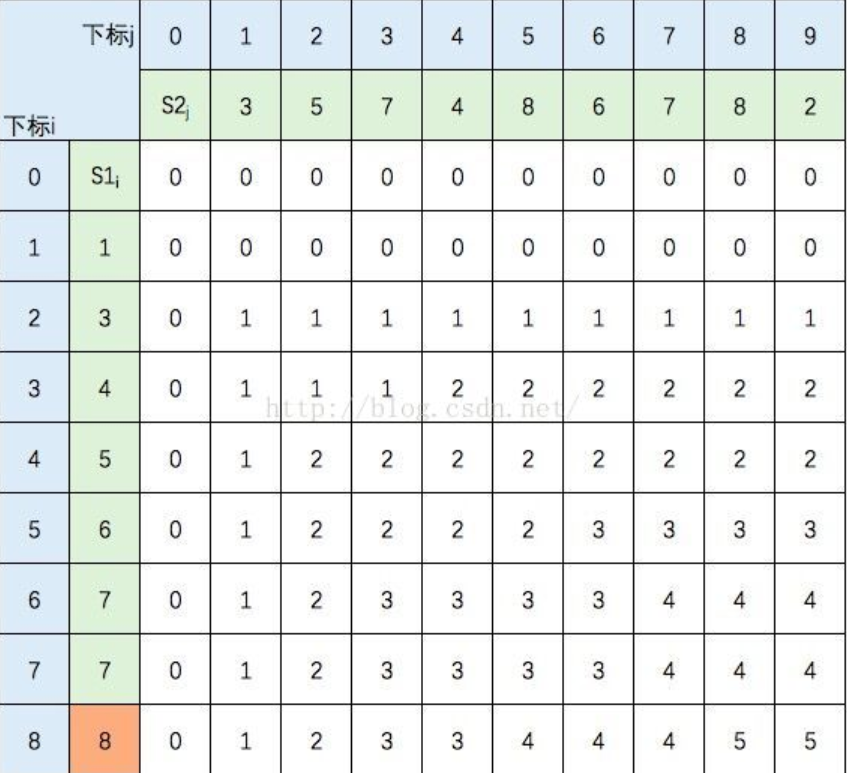
以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。

1.构建二维矩阵A[n+1][n+1] s1为列，s2为行

（1）A[0][any]=0,A[any][0]=0

（2）if(s1[columnIndex-1]==s2[rowIndex-1])则A[rowIndex][columnIndex]=A[rowIndex-1][columnIndex-1]+1;

else  A[rowIndex][columnIndex]=max(A[rowIndex][columnIndex-1],A[rowIndex-1][columnIndex])

（3）由A[8][9]可知最大子序列长度。

图如下：

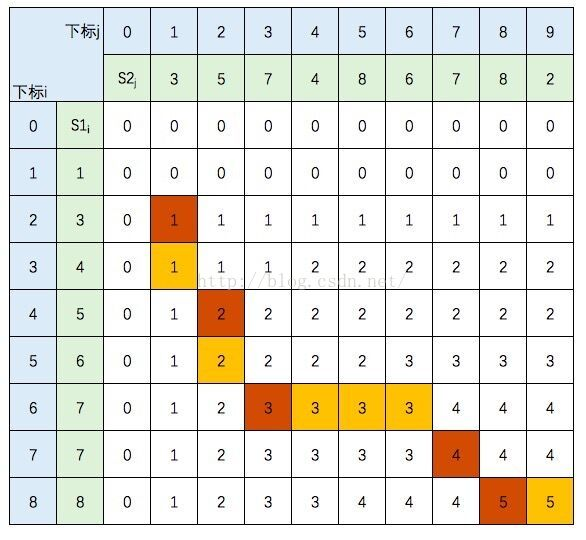
2.针对构建的二维矩阵求最长子序列

（1）当columnIndex>0或者rowIndex>0时。

（2）如果s1[columnIndex-1]==s2[rowIndex-1]则longestSequence.unshift(s1[columnIndex-1]).rowIndex--;columnIndex--.

（3）如果不等，

则1.如果A[rowIndex][columnIndex]==A[rowIndex][columnIndex-1];columnIndex--;//向左

　　　　  2.否则 rowIndex--;

代码如下：

/**
 * @param {string[]} set1
 * @param {string[]} set2
 * @return {string[]}
 */
export default function longestCommonSubsequence(set1, set2) {
  // Init LCS matrix.
  const lcsMatrix = Array(set2.length + ).fill(null).map(() => Array(set1.length + ).fill(null));

  // Fill first row with zeros.
  for (let columnIndex = ; columnIndex <= set1.length; columnIndex += ) {
    lcsMatrix[][columnIndex] = ;
  }

  // Fill first column with zeros.
  for (let rowIndex = ; rowIndex <= set2.length; rowIndex += ) {
    lcsMatrix[rowIndex][] = ;
  }

  // Fill rest of the column that correspond to each of two strings.
  for (let rowIndex = ; rowIndex <= set2.length; rowIndex += ) {
    for (let columnIndex = ; columnIndex <= set1.length; columnIndex += ) {
      if (set1[columnIndex - ] === set2[rowIndex - ]) {
        lcsMatrix[rowIndex][columnIndex] = lcsMatrix[rowIndex - ][columnIndex - ] + ;
      } else {
        lcsMatrix[rowIndex][columnIndex] = Math.max(
          lcsMatrix[rowIndex - ][columnIndex],
          lcsMatrix[rowIndex][columnIndex - ],
        );
      }
    }
  }

  // Calculate LCS based on LCS matrix.
  if (!lcsMatrix[set2.length][set1.length]) {
    // If the length of largest common string is zero then return empty string.
    return [''];
  }

  const longestSequence = [];
  let columnIndex = set1.length;
  let rowIndex = set2.length;

  while (columnIndex >  || rowIndex > ) {
    if (set1[columnIndex - ] === set2[rowIndex - ]) {
      // Move by diagonal left-top.
      longestSequence.unshift(set1[columnIndex - ]);
      columnIndex -= ;
      rowIndex -= ;
    } else if (lcsMatrix[rowIndex][columnIndex] === lcsMatrix[rowIndex][columnIndex - ]) {
      // Move left.
      columnIndex -= ;
    } else {
      // Move up.
      rowIndex -= ;
    }
  }

  return longestSequence;
}