java实现第五届蓝桥杯供水设施

供水设施

X星球的居民点很多。Pear决定修建一个浩大的水利工程，以解决他管辖的N个居民点的供水问题。现在一共有N个水塔，同时也有N个居民点，居民点在北侧从1号到N号自西向东排成一排；水塔在南侧也从1号到N号自西向东排成一排。

N条单向输水线（有水泵动力），将水从南侧的水塔引到北侧对应的居民点。

我们不妨将居民点和水塔都看做平面上的点，居民点坐标为(1,K)_{(N,K)，水塔为(1,0)}(N,0)。

除了N条纵向输水线以外，还有M条单向的横向输水线，连接(Xi,Yi)和(Xi,(Yi)+1)或者(Xi,Yi)和(Xi,(Yi)-1)。前者被称为向右的水路，而后者是向左的。不会有两条水路重叠，即便它们方向不同。

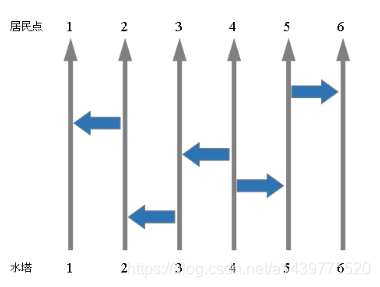
布局的示意图如：【p1.png】所示。

显然，每个水塔的水都可以到达若干个居民点（而不仅仅是对应的那个）。例如上图中，4号水塔可以到达3、4、5、6四个居民点。

现在Pear决定在此基础上，再修建一条横向单项输水线。为了方便考虑，Pear认为这条水路应当是自左向右的，也就是连接了一个点和它右侧的点（例如上图中连接5和6两个纵线的横向水路）。

Pear的目标是，修建了这条水路之后，能有尽可能多对水塔和居民点之间能到达。换句话说，设修建之后第i个水塔能到达Ai个点，你要最大化A1+A2+…+An。

根据定义，这条路必须和X轴平行，但Y坐标不一定要是整数。注意：虽然输入中没有重叠的水路，但是你的方案可以将新修的输水线路与已有的水路重叠。

【输入数据】

输入第一行包含三个正整数N，M，K，含义如题面所述：N是纵向线数，M横向线数，K是居民点纵坐标。

接下来M行，每行三个整数。前两个正整数Xi Yi表示水路的起点坐标；

1<=Xi<=N,0<Yi<K。

接下来一个数0或者1，如果是0表示这条水路向左，否则向右。

保证水路都是合法的，也就是不会流向没有定义的地方。

【输出数据】

输出一行。是一个正整数，即：题目中要求的最大化的A1+A2+…+An。

【输入样例1】

4 3 2

1 1 1

3 1 0

3 1 1

【输出样例1】

11

【输入样例2】

7 9 4

2 3 0

7 2 0

6 3 1

6 1 0

2 1 1

3 3 1

5 2 0

2 2 1

7 1 0

【输出样例2】

21

【数据范围】

对于20%的数据，N,K<=20，M<=100

对于40%的数据，N,K<=100，M<=1000

对于60%的数据，N,K<=1000，M<=100000

对于100%的数据，N,K<=50000，M<=100000

资源约定：

峰值内存消耗（含虚拟机） < 256M

CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意：不要使用package语句。不要使用jdk1.7及以上版本的特性。

注意：主类的名字必须是：Main，否则按无效代码处理。

import java.util.Scanner;

public class Main {
    public static int n, m , k;
    public static int[][] value;

    public void getResult() {
        int max = Integer.MIN_VALUE;
        for(int i = 1;i < n;i++) {
            if(value[i][i+1] == 0) {
                value[i][i+1] = 1;
                int temp = 0;
                for(int k = 1;k <= n;k++) {
                    temp++;
                    int t = k - 1;
                    while(t >= 1) {  //寻找左边连通水磊
                        if(value[t][t+1] == 1) {
                            temp++;
                            t--;
                        } else
                            break;
                    }
                    t = k + 1;
                    while(t <= n) {  //寻找右边连通水磊
                        if(value[t][t-1] == 1) {
                            temp++;
                            t++;
                        } else
                            break;
                    }
                }
                max = Math.max(max, temp);
                value[i][i+1] = 0;
            }
        }
        System.out.println(max);
    }

    public static void main(String[] args) {
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        k = in.nextInt();
        value = new int[n + 1][n + 1];
        for(int i = 0;i < m;i++) {
            int x = in.nextInt();
            @SuppressWarnings("unused")
            double y = in.nextDouble();
            int c = in.nextInt();
            if(c == 0)
                value[x][x - 1] = 1;   //单向向左连通
            else
                value[x][x + 1] = 1;    //单向向右连通
        }
        test.getResult();
    }
}