朱刘算法 有向图定根的最小生成树poj3164

关于为什么不能用Prim求解此类问题，如下

Prim可以看成是维护两个顶点集或者看成维护一颗不断生成的树（感觉前一种说法好一点)

倘若是有向图有三个顶点1.2.3

边的情况如下

1->2:          5

1->3:         6

2->3:       1000861

3->2:         2

显然若是按照Prim算法来说，先将顶点一压入集合。而后顺势找到最小的顶点2，然后1.2中到三的最短边是1000861，那么花费就是1000866，显然不对的。；

而若是无向图则没有这个问题（也就是是说无向图保证最小就是最优），无向图的话找到2，花费5，然后顺势找到3，花费2，这是对的。

以下为转载内容：http://blog.csdn.net/lynnucas/article/details/51305910

最小生成树的具体问题可以用下面的语言阐述：
　　　　输入：一个无向带权图G=(V,E)，对于每一条边(u, v)属于E，都有一个权值w。

　　　　输出：这个图的最小生成树，即一棵连接所有顶点的树，且这棵树中的边的权值的和最小。

　　举例如下，求下图的最小生成树：

　　这个问题是求解一个最优解的过程。那么怎样才算最优呢？

　　首先我们考虑最优子结构：如果一个问题的最优解中包含了子问题的最优解，则该问题具有最优子结构。

　　最小生成树是满足最优子结构的，下面会给出证明：

　　最优子结构描述：假设我们已经得到了一个图的最小生成树(MST) T，(u, v)是这棵树中的任意一条边。如图所示：

　　现在我们把这条边移除，就得到了两科子树T₁和T_{2，如图：}

　　T₁是图G₁=(V₁, E₁)的最小生成树，G₁是由T₁的顶点导出的图G的子图，E₁={(x, y)∈E, x, y ∈V₁}

　　同理可得T₂是图G₂=(V₂, E₂)的最小生成树，G₂是由T₂的顶点导出的图G的子图，E₂={(x, y)∈E, x, y ∈V₂}

　　现在我们来证明上述结论：使用剪贴法。w(T)表示T树的权值和。

　　　　首先权值关系满足：w(T) = w(u, v)+w(T₁)+w(T₂)

　　　　假设存在一棵树T₁'比T₁更适合图G1，那么就存在T'={(u,v)}UT₁'UT₂'，那么T'就会比T更适合图G，这与T是最优解相矛盾。得证。

　　因此最小生成树具有最优子结构，那么它是否还具有重叠子问题性质呢？我们可以发现，不管删除那条边，上述的最优子结构性质都满足，都可以同样求解，因此是满足重叠子问题性质的。

　　考虑到这，我们可能会想：那就说明最小生成树可以用动态规划来做咯？对，可以，但是它的代价是很高的。

　　我们还能发现，它还有个更强大的性质：贪心选择性质。因而可用贪心算法完成。

　　贪心算法特点：一个局部最优解也是全局最优解。

　　最小生成树的贪心选择性质：令T为图G的最小生成树，另A⊆V，假设边(u, v)∈E是连接着A到A的补集（也就是V-A)的最小权值边，那么(u, v)属于最小生成树。

　　证明：假设(u, v)∉T， 使用剪贴法。现在对下图进行分析，图中A的点用空心点表示，V-A的点用实心点表示：

　　在T树中，考虑从u到v的一条简单路径（注意现在(u, v)不在T中），根据树的性质，它是唯一的。

　   现在把(u, v)和这条路上中的第一条连接A和V-A的边交换，即画红杠的那条边，边(u, v)是连接A和V-A的权值最小边，那我们就得到了一棵更小的树，这就与T是最小　　生成树矛盾。得证。

　　现在呢，我们来看看Prim的思想：Prim算法的特点是集合E中的边总是形成单棵树。树从任意根顶点s开始，并逐渐形成，直至该树覆盖了V中所有顶点。每次添加到树中的边都是使树的权值尽可能小的边。因而上述策略是“贪心”的。

我是大自然的搬运工 -----http://blog.csdn.net/wsniyufang/article/details/6747392

最 小树形图，就是给有向带权图中指定一个特殊的点root，求一棵以root为根的有向生成树T，并且T中所有边的总权值最小。最小树形图的第一个算法是 1965年朱永津和刘振宏提出的复杂度为O(VE)的算法。
判断是否存在树形图的方法很简单，只需要以v为根作一次图的遍历就可以了，所以下面的 算法中不再考虑树形图不存在的情况。
在所有操作开始之前，我们需要把图中所有的自环全都清除。很明显，自环是不可能在任何一个树形图上的。只有进 行了这步操作，总算法复杂度才真正能保证是O(VE)。
首先为除根之外的每个点选定一条入边，这条入边一定要是所有入边中最小的。现在所有的最小 入边都选择出来了，如果这个入边集不存在有向环的话，我们可以证明这个集合就是该图的最小树形图。这个证明并不是很难。如果存在有向环的话，我们就要将这 个有向环所称一个人工顶点，同时改变图中边的权。假设某点u在该环上，并设这个环中指向u的边权是in[u]，那么对于每条从u出发的边(u, i, w)，在新图中连接(new, i, w)的边，其中new为新加的人工顶点; 对于每条进入u的边(i, u, w)，在新图中建立边(i, new, w-in[u])的边。为什么入边的权要减去in[u]，这个后面会解释，在这里先给出算法的步骤。然后可以证明，新图中最小树形图的权加上旧图中被收缩 的那个环的权和，就是原图中最小树形图的权。
上面结论也不做证明了。现在依据上面的结论，说明一下为什么出边的权不变，入边的权要减去in [u]。对于新图中的最小树形图T，设指向人工节点的边为e。将人工节点展开以后，e指向了一个环。假设原先e是指向u的，这个时候我们将环上指向u的边 in[u]删除，这样就得到了原图中的一个树形图。我们会发现，如果新图中e的权w'(e)是原图中e的权w(e)减去in[u]权的话，那么在我们删除 掉in[u]，并且将e恢复为原图状态的时候，这个树形图的权仍然是新图树形图的权加环的权，而这个权值正是最小树形图的权值。所以在展开节点之后，我们 得到的仍然是最小树形图。逐步展开所有的人工节点，就会得到初始图的最小树形图了。
如果实现得很聪明的话，可以达到找最小入边O(E)，找环 O(V)，收缩O(E)，其中在找环O(V)这里需要一点技巧。这样每次收缩的复杂度是O(E)，然后最多会收缩几次呢？由于我们一开始已经拿掉了所有的 自环，我门可以知道每个环至少包含2个点，收缩成1个点之后，总点数减少了至少1。当整个图收缩到只有1个点的时候，最小树形图就不不用求了。所以我们最 多只会进行V-1次的收缩，所以总得复杂度自然是O(VE)了。由此可见，如果一开始不除去自环的话，理论复杂度会和自环的数目有关。
======================== 分割线之上摘自Sasuke_SCUT的blog=====================================================

下 面是朱刘算法的构造图

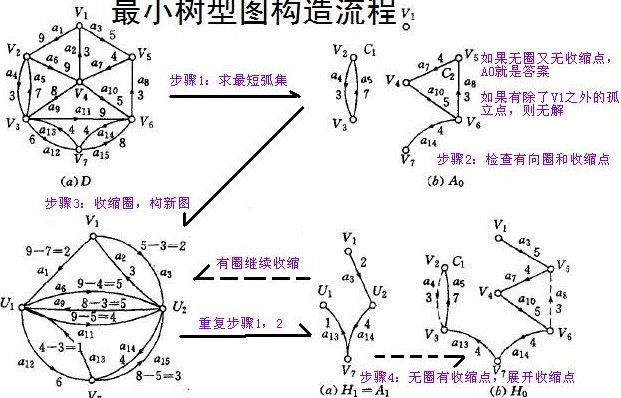
#include <cstdio>
#include <iostream>
#include<queue>
#include<set>
#include<ctime>
#include<algorithm>
#include<cmath>
#include<vector>
#include<map>
#include<cstring>
using namespace std;
const double eps=1e-;
#define M 109
#define type double
const type inf=()<<;
struct point
{
    double x,y;
}p[M];
double dis(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
struct Node{
    int u , v;
    type cost;
}E[M*M+];
int pre[M],ID[M],vis[M];
type In[M];
int n,m;
type Directed_MST(int root,int NV,int NE) {
    type ret = ;
    while(true) {
        //1.找最小入边
        for(int i=;i<NV;i++) In[i] = inf;
        for(int i=;i<NE;i++){
            int u = E[i].u;
            int v = E[i].v;
            if(E[i].cost < In[v] && u != v) {
                pre[v] = u;
                In[v] = E[i].cost;
            }
        }
        for(int i=;i<NV;i++) {
            if(i == root) continue;
            if(In[i] == inf)    return -;//除了跟以外有点没有入边,则根无法到达它
        }
        //2.找环
        int cntnode = ;
    //    CC(ID,-1);
    //    CC(vis,-1);
    memset(ID,-,sizeof(ID));
    memset(vis,-,sizeof(vis));
        In[root] = ;
        for(int i=;i<NV;i++) {//标记每个环
            ret += In[i];
            int v = i;
            while(vis[v] != i && ID[v] == - && v != root) {
                vis[v] = i;
                v = pre[v];
            }
            if(v != root && ID[v] == -) {
                for(int u = pre[v] ; u != v ; u = pre[u]) {
                    ID[u] = cntnode;
                }
                ID[v] = cntnode ++;
            }
        }
        if(cntnode == )    break;//无环
        for(int i=;i<NV;i++) if(ID[i] == -) {
            ID[i] = cntnode ++;
        }
        //3.缩点,重新标记
        for(int i=;i<NE;i++) {
            int v = E[i].v;
            E[i].u = ID[E[i].u];
            E[i].v = ID[E[i].v];
            if(E[i].u != E[i].v) {
                E[i].cost -= In[v];
            }
        }
        NV = cntnode;
        root = ID[root];
    }
    return ret;
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        // memset(pre,0,sizeof(pre));
        for(int i=;i<n;i++)
        scanf("%lf%lf",&p[i].x,&p[i].y);
        for(int i=;i<m;i++)
        {
        scanf("%d%d",&E[i].u,&E[i].v);
        E[i].u--;
        E[i].v--;
        if(E[i].u!=E[i].v)
        E[i].cost=dis(p[E[i].u],p[E[i].v]);
        else E[i].cost=<<;
        }
        type ans=Directed_MST(,n,m);
        if(ans==-)
        printf("poor snoopy\n");
        else
        printf("%.2f\n",ans);
    }
    return ;
}