MySql索引机制

第一部分 MySQL数据库索引的数据结构及算法理论

第二部分 MySQL索引实现机制

第三部分 MySQL中高性能使用索引的策略

数据结构及算法

MySQL官方对索引的定义为：索引（Index）是帮助MySQL高效获取数据的数据结构。

查询算法的进化：

顺序查找（linear search）时间复杂度为O(n) ====》优化查找算法（二分查找（binary search）、二叉树查找（binary tree search）等）

问题来了：查找效率提高了，但是各自对检索的数据都有要求：二分查找要求被检索数据有序，而二叉树查找只能应用于二叉查找树上，但是数据本身的组织结构不可能完全满足各种数据结构（例如，理论上不可能同时将两列都按顺序进行组织）

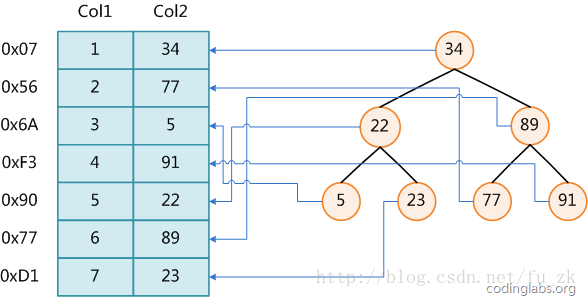
上图展示了一种可能的索引方式。左边是数据表，一共有两列七条记录，最左边的是数据记录的物理地址（注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的）。为了加快Col2的查找，可以维护一个右边所示的二叉查找树，每个节点分别包含索引键值和一个指向对应数据记录物理地址的指针，这样就可以运用二叉查找；但是实际的数据库系统几乎没有使用二叉查找树或其进化品种红黑树（red-black tree）实现的，原因会在下文介绍。

B-Tree和B+Tree

目前大部分数据库系统及文件系统都采用B-Tree或其变种B+Tree作为索引结构，在下一节会结合存储器原理及计算机存取原理讨论为什么B-Tree和B+Tree在被如此广泛用于索引。

B-Tree

定义一条数据记录为一个二元组[key, data]，key为记录的键值，对于不同数据记录，key是互不相同的；data为数据记录除key外的数据。B-Tree是满足下列条件的数据结构：

d>=2，即B-Tree的度；
h为B-Tree的高；
每个非叶子结点由n-1个key和n个指针组成，其中d<=n<=2d；
每个叶子结点至少包含一个key和两个指针，最多包含2d-1个key和2d个指针，叶结点的指针均为NULL；
所有叶结点都在同一层，深度等于树高h；
key和指针相互间隔，结点两端是指针；
一个结点中的key从左至右非递减排列；
如果某个指针在结点node最左边且不为null，则其指向结点的所有key小于
如果某个指针在结点node最右边且不为null，则其指向结点的所有key大于
如果某个指针在结点node的左右，相邻key分别是指向节点的上下界限

如下图是一个 d=2的B-Tree

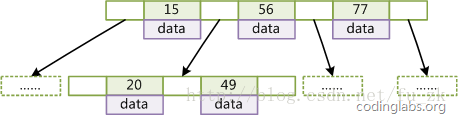
B+Tree

B-Tree有许多变种，其中最常见的是B+Tree，例如MySQL就普遍使用B+Tree实现其索引结构

由于并不是所有节点都具有相同的域，因此B+Tree中叶结点和内结点一般大小不同。这点与B-Tree不同，虽然B-Tree中不同节点存放的key和指针可能数量不一致，但是每个结点的域和上限是一致的，所以在实现中B-Tree往往对每个结点申请同等大小的空间。

B+Tree比B-Tree更适合实现外存储索引结构，具体原因与外存储器原理及计算机存取原理有关。

参照：https://www.cnblogs.com/dongguacai/p/7239599.html

B-/+Tree索引的性能分析

从使用磁盘I/O次数评价索引结构的优劣性：根据B-Tree的定义，可知检索一次最多需要访问h个结点。数据库系统的设计者巧妙的利用了磁盘预读原理，将一个结点的大小设为等于一个页面，这样每个结点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：

每次新建结点时，直接申请一个页面的空间，这样可以保证一个结点的大小等于一个页面，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。

B-Tree中一次检索最多需要h-1次I/O（根结点常驻内存），渐进复杂度为O(h)=O(log_dN)。一般实际应用中，出读d是非常大的数字，通常超过100，因此h非常小。

综上所述，用B-Tree作为索引结构效率是非常高的。

而红黑树结构，h明显要深得多。由于逻辑上很近的结点（父子结点）物理上可能离得很远，无法利用局部性原理。所以即使红黑树的I/O渐进复杂度也为O(h)，但是查找效率明显比B-Tree差得多。

MySQL索引实现

MyIASM引擎的索引结构

　　前面已经说过，索引存储的是[key, value]，key是建立索引的数据列，value是存储的数据域。MyIASM引擎的数据域内容是数据实际物理地址，这种与实际数据分离的索引即是 非聚集索引。

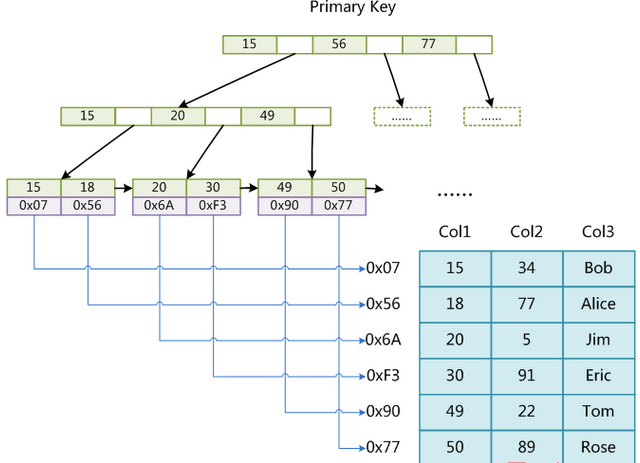
上图中数据表一共有三列，Col1为主键，则上图是一个MyISAM表的主索引（Primary key）示意图。在MyISAM中，主索引和辅助索引（Secondary key）在结构上没有任何区别，只是主索引要求key是唯一的，而辅助索引的key可以重复。

MyISAM中索引检索的算法为首先按照B+Tree搜索算法搜索索引，如果指定的Key存在，则取出其data域的值，然后以data域的值为地址，读取相应数据记录。

InnoDB引擎的索引结构

InnoDB引擎的[key, value]中，value存储的是实际数据，这种索引也叫聚集索引。

如下图所示，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键，因此InnoDB表数据文件本身就是主索引。

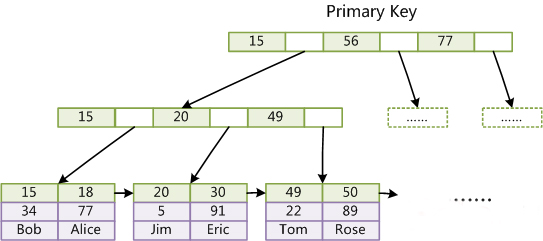
InnoDB的数据文件本身要按主键聚集，所以InnoDB要求表必须有主键（MyISAM可以没有），如果没有显式指定，则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键，如果不存在这种列，则MySQL自动为InnoDB表生成一个隐含字段作为主键。

与MyISAM索引的不同是InnoDB的辅助索引data域存储相应记录主键的值而不是地址。换句话说，InnoDB的所有辅助索引都引用主键作为data域。如下图所示：

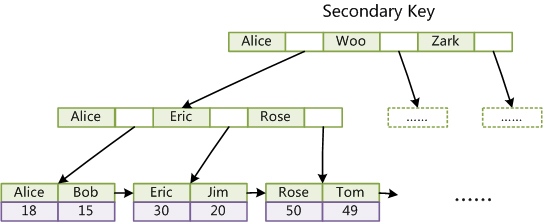
这里以英文字符的ASCII码作为比较准则。聚集索引这种实现方式使得按主键的搜索十分高效，但是辅助索引搜索需要检索两遍索引：首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录。