L - Kakuro Extension - HDU 3338 - （最大流）

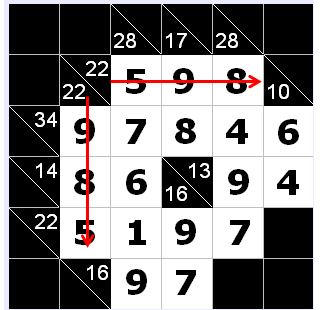
题意：有一个填数字的游戏，需要你为白色的块内填一些值，不过不能随意填的，是有一些规则的（废话），在空白的上方和作方给出一些值，如果左下角有值说明下面列的和等于这个值，右上角的值等于这行后面的数的和，如下图示，现在把空白的地方填上数字即可（只能填从1~9的数字，不限制一行是否有重复数字）。

分析：如果这道题不在网络流专题里面估计很难向网络流这样面去想（看不出来），不过如果刻意往这个地方想的话还是能想到的，首先可以观察出来行的和等于列的和，所以用行和列的一边当源一边当汇，然后用每个白块与相对应的行列相连，因为最大流量是9，最少的点流量也得是1，为了防止0流量出现，让每个白块的最大流量是8，与之相对应的行列都要减去一些值（有几个白块就减去几），输出的时候让所有的值再加上1，这样所有的值就符合要求了，我处理的时候把白块拆点了（仔细想一下不拆也没事，因为每个白块只有两条边与它相连，一个进一个出，写的还是有些麻烦了）。

下面是AC代码

***********************************************************************************************************************************************************

#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
using namespace std;

const int MAXN = ;
const int oo = 1e9+;

struct Graph
{///描述点的属性，是黑色还是白色，是行和还是列的和
///并且给他们编号（为了节约内存的设置，也可以直接用下标编号）
    int rowSum, rIndex;
    int polSum, pIndex;
    int white, wIndex;
}G[MAXN][MAXN];
struct Edge{int v, flow, next;}edge[MAXN*MAXN*MAXN];
int Head[MAXN*MAXN*], cnt, Layer[MAXN*MAXN*];
int Row, Pol, White;///这些块总数

void InIt()
{
    cnt = Row = Pol = White = ;
    memset(Head, -, sizeof(Head));
    memset(G, , sizeof(G));
}
void Trun(char s[], Graph &p)
{
    if(strcmp(s, "XXXXXXX") == )
        return ;
    if(strcmp(s, ".......") == )
    {
        p.white = true;
        p.wIndex = ++White;
        return ;
    }

    s[] = ;

    if(s[] >= '' && s[] <= '')
    {///前面的是列值
        sscanf(s, "%d", &p.polSum);
        p.pIndex = ++Pol;
    }
    if(s[] >= '' && s[] <= '')
    {///后面是行
        sscanf(s+, "%d", &p.rowSum);
        p.rIndex = ++Row;
    }
}
void AddEdge(int u, int v, int flow)
{
    edge[cnt].v = v;
    edge[cnt].flow = flow;
    edge[cnt].next = Head[u];
    Head[u] = cnt++;

    swap(u, v);

    edge[cnt].v = v;
    edge[cnt].flow = ;
    edge[cnt].next = Head[u];
    Head[u] = cnt++;
}
bool BFS(int start, int End)
{
    memset(Layer, , sizeof(Layer));
    queue<int>Q;
    Q.push(start);
    Layer[start] = ;

    while(Q.size())
    {
        int u = Q.front();Q.pop();

        if(u == End)return true;

        for(int j=Head[u]; j!=-; j=edge[j].next)
        {
            int v = edge[j].v;

            if(Layer[v] == false && edge[j].flow)
            {
                Layer[v] = Layer[u] + ;
                Q.push(v);
            }
        }
    }

    return false;
}
int DFS(int u, int MaxFlow, int End)
{
    if(u == End)return MaxFlow;

    int uflow = ;

    for(int j=Head[u]; j!=-; j=edge[j].next)
    {
        int v = edge[j].v;

        if(Layer[v]-==Layer[u] && edge[j].flow)
        {
            int flow = min(MaxFlow-uflow, edge[j].flow);
            flow = DFS(v, flow, End);

            edge[j].flow -= flow;
            edge[j^].flow += flow;
            uflow += flow;

            if(uflow == MaxFlow)
                break;
        }
    }

    if(uflow == )
        Layer[u] = ;

    return uflow;
}
int Dinic(int start, int End)
{
    int MaxFlow = ;

    while(BFS(start, End) == true)
        MaxFlow += DFS(start, oo, End);

    return MaxFlow;
}

int main()
{
    int M, N;

    while(scanf("%d%d", &M, &N) != EOF)
    {
        int i, j, k, q;
        char s[];

        InIt();

        for(i=; i<=M; i++)
        for(j=; j<=N; j++)
        {
            scanf("%s", s);
            Trun(s, G[i][j]);
        }

        int start = Row+Pol+White*+, End = start+;
        int Ri = White*, Pi = Ri+Row;;

        for(i=; i<=M; i++)
        for(j=; j<=N; j++)
        {
            if(G[i][j].rowSum > )
            {///把源点与行连接,流量就是行的和
                k = G[i][j].rIndex;
                AddEdge(start, Ri+k, G[i][j].rowSum);
                q = cnt - ;///记录下这条边的下标
            }
            if(G[i][j].white == true)
            {///如果是白色的块,与所连的行的流量减1

                int t = G[i][j].wIndex;

                edge[q].flow -= ;
                AddEdge(Ri+k, t, );///点与前面所在的行相连
                AddEdge(t, t+White, );///把白色拆点
                G[i][j].pIndex = cnt - ;///记录拆的那条边
            }
        }

        for(j=; j<=N; j++)
        for(i=; i<=M; i++)
        {
            if(G[i][j].polSum > )
            {///把汇点与列相连
                k = G[i][j].pIndex;
                AddEdge(Pi+k, End, G[i][j].polSum);
                q = cnt - ;
            }
            if(G[i][j].white == true)
            {///如果是白色块，与之相连的列的流量减1
                int t = G[i][j].wIndex;

                edge[q].flow -= ;
                AddEdge(White+t, Pi+k, );///拆点与前面所在的列相连
            }
        }
        Dinic(start, End);
        ///printf("%d\n",Dinic(start, End));

        for(i=; i<=M; i++)
        for(j=; j<=N; j++)
        {
            if(G[i][j].white == true)
            {
                int t = G[i][j].pIndex;
                printf("%d", edge[t].flow+);
            }
            else
                printf("_");

            printf("%c", j==N ? '\n' : ' ');
        }
    }

    return ; }