哈夫曼树（Huffman）的JS实现

我本身并不懂哈夫曼树也不知道有什么用，GOOGLE了下，也只是一知半解，只是刚好看到有JAVA实现版，又看了下生成原理，感觉挺有意思，就写了一下

有些地方可以优化，效率不怎么样的，纯好玩，也不保证一定正确，只是测试了现有数据，有答案一样而已

 //用于测试数据
 var arr = [1,2,3,4,5,6]

 //哈夫曼树类
 function Huffman (left,right) {
     this.left = left; //左子节点
     this.right = right; //右子节点
 }

 //节点值
 Huffman.prototype.val = function() {
     return (this.left.val ? this.left.val() : this.left) + (this.right.val ? this.right.val() : this.right);
 };

 //生成
 //list：用于生成的值，数组类型
 Huffman.create = function (list) {
     while(list.length>1){
         list.sort(function(a,b){
             a = a.val ? a.val() : a;
             b = b.val ? b.val() : b;
             return a-b;
         });

         var item = new Huffman(list.shift(),list.shift());
         list.push(item);
     }
     return list[0]
 }

 //示例
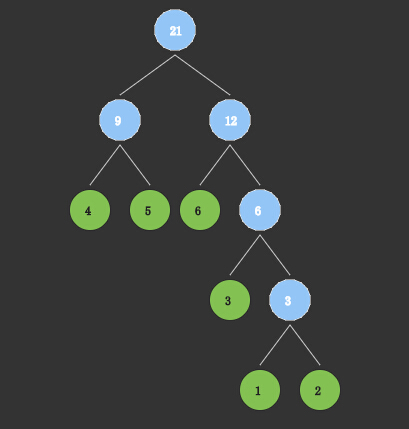
 var huff = Huffman.create(arr);

用Canvas画的树，绿色表示原始值