算法学习笔记【6】| KMP 算法

KMP（Knuth-Morris-Pratt字符串查找算法）

KMP 算法是可以快速在文本串 s 中找到模式串 a 的算法。

Part 1:幼稚的算法

首先思考我们在暴力匹配模式串时的思路：

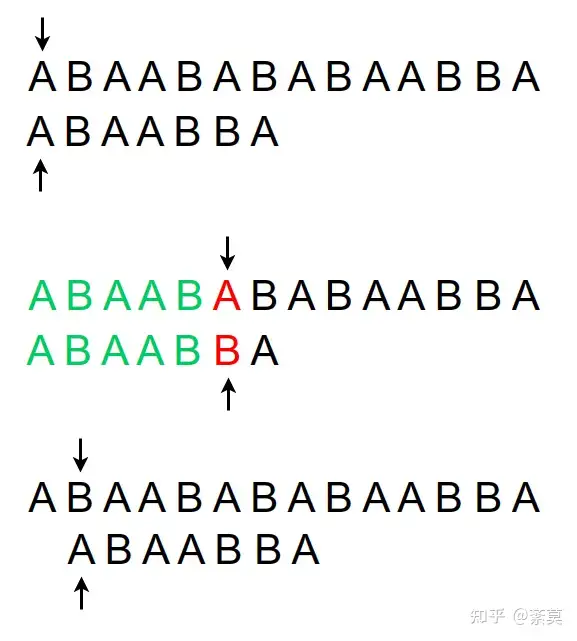
一旦有一位失配，就需要整个回溯，导致时间复杂度超标。

而 KMP 算法主要就是优化了这个回溯的问题。

一个人有多强不在于他能在顺境时走得多远，而在于他在逆境时能多久找回曾经的自己。

KMP 算法

首先我们要考虑让某个点不回溯，再优化另一个点的回溯过程。

KMP 给出了这样的一种方式：

设 i 表示文本串的位置，j 表示模式串的位置，我们让 i 不动，j 回溯到最合适的位置，这个位置，我们记为PMT（Partial Match Table，部分匹配表）。

PMT 数组的含义，也可以这样表示：

1 到 j 子串的最长公共前后缀长度。

就像这样：

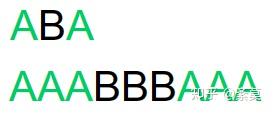
当然，最长前后缀是可以重叠的：

那就有个问题，难道最长的不是整个串吗？所以为了避免卡 bug，PMT 要求这个公共前后缀的长度要小于子串长度。

我们在考虑一开始那个发生失配的情况，用 KMP 算法就可以变成这样：

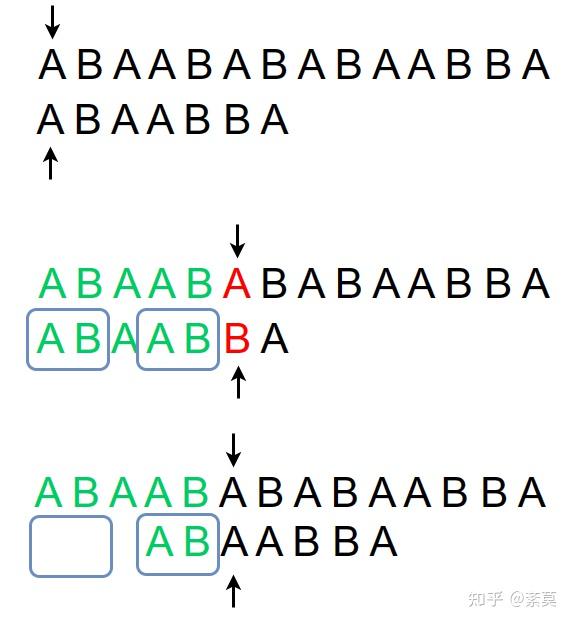
实际上我们没有移动 i，只是让 j 变成了 pmt[j-1]。
如果这一位继续失配，那么 j 又变成了 pmt[j-1]。

反复如此，直到不得不移动 i 为止。

那么代码可以写成这样：

for(int i=0,j=0;i<s.size();i++){

    while(j && s[i] != a[j])

        j = pmt[j-1];

    if(s[i] == a[j]) j++;

    if(j == a.size())

        j = pmt[j-1];

}

对于每一位首先处理失配的情况，然后判断是否能匹配当前位置，特别的是当 j 匹配完后（匹配成功），就需要准备下一次匹配，也可以理解为 j 的下一位（空）和 i 的下一位失配了。

不过我们上面的代码是假设 pmt 数组已经求出，别忘了求出 pmt 本身也不简单。

一个精妙的方法是进行模式串的自匹配。首先将模式串错开一位，然后和自己匹配一次，这样每次匹配的最大长度就刚好是公共前后缀的长度！

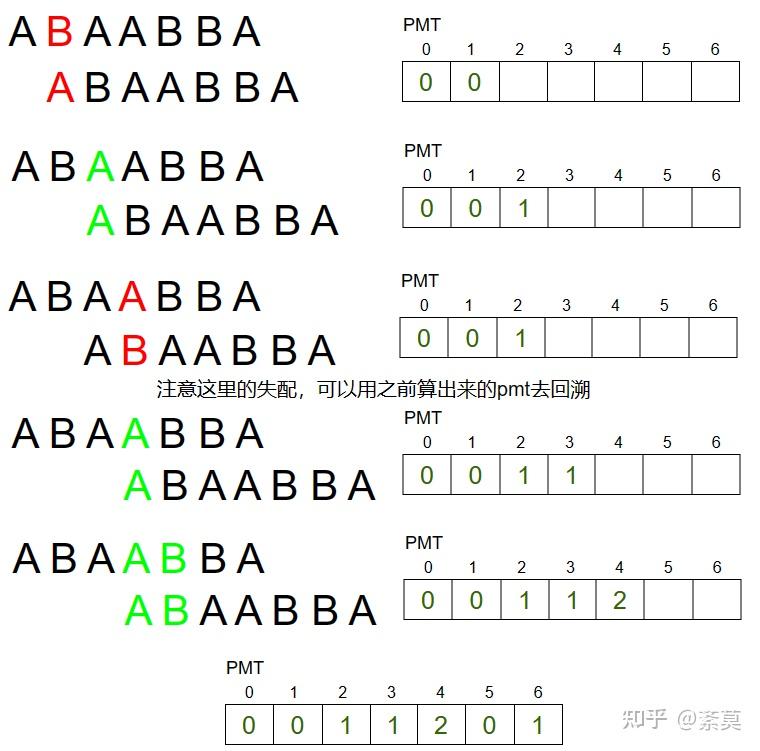
代码如下：

#include <bits/stdc++.h>

using namespace std;

int main(){

    string a;

    cin>>a;

    int pmt[114]={0};

    for(int i=1,j=0;i<a.size();i++){

        while(j && a[i] != a[j])

            j = pmt[j-1];

        if(a[i] == a[j]) j++;

        pmt[i] = j;

    }

    for(int i=0;i<a.size();i++){

        cout<<pmt[i]<<' ';

    }

    return 0;

}

例题和代码

P3375 【模板】KMP 字符串匹配

border 其实就是 pmt 数组。

const int N=1000005;

int pmt[N];

int main(){

    ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);

    string s,a;

    cin>>s>>a;

    for(int i=1,j=0;i<a.size();i++){

        while(j && a[i] != a[j])

            j = pmt[j-1];

        if(a[i] == a[j]) j++;

        pmt[i] = j;

    }

    for(int i=0,j=0;i<s.size();i++){

        while(j && s[i] != a[j])

            j = pmt[j-1];

        if(s[i] == a[j]) j++;

        if(j == a.size()){

            cout<<i+1-(a.size()-1)<<endl;

            j = pmt[j-1];

        }

    }

    for(int i=0;i<a.size();i++){

        cout<<pmt[i]<<' ';

    }

    return 0;

}