再谈汤普森采样（Thompson Sampling）

相关：

【转载】 推荐算法之Thompson(汤普森)采样

【转载】 推荐系统 EE 问题与 Bandit 算法

python语言绘图：绘制一组beta分布图

转载： beta分布介绍

python语言绘图：绘制一组以beta分布为先验，以二项分布为似然的贝叶斯后验分布图

深入理解什么是Beta分布

在线学习(MAB)与强化学习(RL)[2]：IID Bandit的一些算法

外网教程：

https://web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf

国内教程：

强化学习理论基础 4.8 汤普森采样（Thompson Sampling）

=====================================

之前已经share了多篇相关的post，最近看到了一个新的这方面的东西，就想着再谈下这个问题。汤普森采样（Thompson Sampling）是MAB（Multi arm bandit）问题中经常被讨论的一种均衡exploit和explore的方法，之前已经解释了很多相关的资料，最近看到了些不一样的东西，之前share的汤普森采样（Thompson Sampling）都是使用beta分布做先验和后验的，不过发现最近发现也有使用正态分布做先验和后验的。

根据维基百科上的Thompson sampling的定义：

可以看到，汤普森采样（Thompson Sampling）并不是一定要用beta分布的，汤普森采样（Thompson Sampling）其实核心就是利用贝叶斯公式在抽样时评估哪个抽样的最优可能性更高。我们在使用汤普森采样（Thompson Sampling）时需要先设置先验概率分布和似然概率分布，而且我们还需要保证获得的后验概率分布和先验概率分布是共轭的，这样就可以不断的根据抽样的次数来进行迭代评估。我们最常用的汤普森采样（Thompson Sampling）就是伯努利-汤普森采样（Bernoulli Thompson Sampling），也就是使用beta分布作为先验分布和后验分布，使用二项分布作为似然函数的方法，大致形式的伪代码如下：

伯努利-汤普森采样（Bernoulli Thompson Sampling）

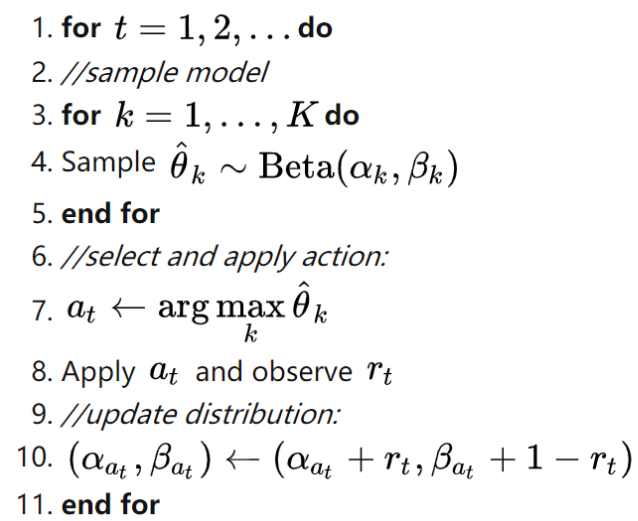
其中的核心代码为： （参考：https://zhuanlan.zhihu.com/p/36199435）

import  numpy as np

import  pymc

# wins 和 trials 都是一个 N 维向量，N 是臂的个数

# wins 表示所有臂的 α 参数，loses 表示所有臂的 β 参数

choice = np.argmax(pymc.rbeta(1 + wins, 1 + loses, len(wins)))

可以看到，伯努利-汤普森采样（Bernoulli Thompson Sampling）很大的一个局限性就是使用二项分布作为似然函数，因为这样我们每次抽样的结果都只能是0或1，也就是发生或没发生，而在MAB（Multi arm bandit）问题中我们采样的reward的形式有的时候是0或1，但是也存在多个离散值，甚至是连续值的reward，这样就不适用伯努利-汤普森采样（Bernoulli Thompson Sampling），该种情况下我们可以使用高斯-汤普森采样（Gaussian  Thompson Sampling）。

高斯-汤普森采样（Gaussian  Thompson Sampling）

这里不给出具体的数学推导公式及证明了，原有有两点：1.是没有那么多精力写这些旁支内容；2.是本人也确实不会这东西的推导和证明。

直接给出Python代码：（https://github.com/mimoralea/gdrl）

def thompson_sampling(env,
                      alpha=1,
                      beta=0,
                      n_episodes=1000):
    Q = np.zeros((env.action_space.n), dtype=np.float64)
    N = np.zeros((env.action_space.n), dtype=np.int)

    Qe = np.empty((n_episodes, env.action_space.n), dtype=np.float64)
    returns = np.empty(n_episodes, dtype=np.float64)
    actions = np.empty(n_episodes, dtype=np.int)
    name = 'Thompson Sampling {}, {}'.format(alpha, beta)
    for e in tqdm(range(n_episodes),
                  desc='Episodes for: ' + name,
                  leave=False):
        samples = np.random.normal(
            loc=Q, scale=alpha/(np.sqrt(N) + beta))
        action = np.argmax(samples)

        _, reward, _, _ = env.step(action)
        N[action] += 1
        Q[action] = Q[action] + (reward - Q[action])/N[action]

        Qe[e] = Q
        returns[e] = reward
        actions[e] = action
    return name, returns, Qe, actions

核心代码部分：

也就是说，高斯-汤普森采样（Gaussian  Thompson Sampling）是使用正态分布作为先验和后验的，每次抽样后我都只需要更新对应arm的正态分布中的均值和方差即可。需要注意的是高斯分布也是共轭分布。

--------------------------------------------------

在外网找到了些关于汤普森采样（Thompson Sampling）不错的资料：

https://towardsdatascience.com/thompson-sampling-fc28817eacb8

https://web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf

====================================

同时也给出其他的采样方法：

softmax采样：

def softmax(env,
            init_temp=float('inf'),
            min_temp=0.0,
            decay_ratio=0.04,
            n_episodes=1000):
    Q = np.zeros((env.action_space.n), dtype=np.float64)
    N = np.zeros((env.action_space.n), dtype=np.int)

    Qe = np.empty((n_episodes, env.action_space.n), dtype=np.float64)
    returns = np.empty(n_episodes, dtype=np.float64)
    actions = np.empty(n_episodes, dtype=np.int)
    name = 'Lin SoftMax {}, {}, {}'.format(init_temp,
                                           min_temp,
                                           decay_ratio)
    # can't really use infinity
    init_temp = min(init_temp,
                    sys.float_info.max)
    # can't really use zero
    min_temp = max(min_temp,
                   np.nextafter(np.float32(0),
                                np.float32(1)))
    for e in tqdm(range(n_episodes),
                  desc='Episodes for: ' + name,
                  leave=False):
        decay_episodes = n_episodes * decay_ratio
        temp = 1 - e / decay_episodes
        temp *= init_temp - min_temp
        temp += min_temp
        temp = np.clip(temp, min_temp, init_temp)

        scaled_Q = Q / temp
        norm_Q = scaled_Q - np.max(scaled_Q)
        exp_Q = np.exp(norm_Q)
        probs = exp_Q / np.sum(exp_Q)
        assert np.isclose(probs.sum(), 1.0)

        action = np.random.choice(np.arange(len(probs)),
                                  size=1,
                                  p=probs)[0]

        _, reward, _, _ = env.step(action)
        N[action] += 1
        Q[action] = Q[action] + (reward - Q[action])/N[action]

        Qe[e] = Q
        returns[e] = reward
        actions[e] = action
    return name, returns, Qe, actions

上置信采样Upper confidence bound(UCB)：

def upper_confidence_bound(env,
                           c=2,
                           n_episodes=1000):
    Q = np.zeros((env.action_space.n), dtype=np.float64)
    N = np.zeros((env.action_space.n), dtype=np.int)

    Qe = np.empty((n_episodes, env.action_space.n), dtype=np.float64)
    returns = np.empty(n_episodes, dtype=np.float64)
    actions = np.empty(n_episodes, dtype=np.int)
    name = 'UCB {}'.format(c)
    for e in tqdm(range(n_episodes),
                  desc='Episodes for: ' + name,
                  leave=False):
        action = e
        if e >= len(Q):
            U = c * np.sqrt(np.log(e)/N)
            action = np.argmax(Q + U)

        _, reward, _, _ = env.step(action)
        N[action] += 1
        Q[action] = Q[action] + (reward - Q[action])/N[action]

        Qe[e] = Q
        returns[e] = reward
        actions[e] = action
    return name, returns, Qe, actions

注意本文中定义的Python函数块内代码内容遵守BSD 3-Clause License协议，协议内容：

BSD 3-Clause License

Copyright (c) 2018, Miguel Morales
All rights reserved.

Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:

* Redistributions of source code must retain the above copyright notice, this
  list of conditions and the following disclaimer.

* Redistributions in binary form must reproduce the above copyright notice,
  this list of conditions and the following disclaimer in the documentation
  and/or other materials provided with the distribution.

* Neither the name of the copyright holder nor the names of its
  contributors may be used to endorse or promote products derived from
  this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE
FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY,
OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE
OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.