hihoCoder 后缀自动机三·重复旋律6

后缀自动机三·重复旋律6

时间限制:15000ms

单点时限:3000ms

内存限制:512MB

描述

小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为一段数构成的数列。

现在小Hi想知道一部作品中所有长度为K的旋律中出现次数最多的旋律的出现次数。但是K不是固定的，小Hi想知道对于所有的K的答案。

解题方法提示

输入

共一行，包含一个由小写字母构成的字符串S。字符串长度不超过 1000000。

输出

共Length(S)行，每行一个整数，表示答案。

样例输入

aab

样例输出

2
1
1

小Hi：上次我们已经学习了后缀自动机了，今天我们再来解决一个用到后缀自动机的问题。

小Ho：好！那我们开始吧！

小Hi：现在我们要对K=1..length(S)求出所有长度为K的子串中出现次数最多的子串的出现次数。小Ho你有什么想法么？

小Ho：我有一个Naive的想法。在上上周我们已经知道对于SAM中的一个状态st，endpos(st)就是st这个状态包含的子串在S中的所有结束位置（st包含所有子串都具有相同的结束位置集合）。每个不同的结束位置就对应了一次出现次数。所以如果我们能在构造SAM的过程中把endpos也都求出来，应该就能解决这个问题了。

小Hi：你这个思路不错，但是复杂度有些高。我们用|endpos(st)|表示endpos(st)的大小。那么对于一个状态st，|endpos(st)|最坏可能到达O(length(S))的级别，所有状态的|endpos(st)|之和最坏也可能达到O(length(S)^2)级别。

小Hi：比如对于S="aaaaa"，其状态如下，容易发现Σ|endpos(st)| = 1 + 2 + 3 + ...。

状态	子串	endpos
S	空串
1	a	{1,2,3,4,5}
2	aa	{2,3,4,5}
3	aaa	{3,4,5}
4	aaaa	{4,5}
5	aaaaa	{5}

小Ho：所以如果我们对每个状态维护endpos的话，复杂度至少也是O(length(S)^2)的哦？那我们能不能只维护endpos(st)的大小，即|endpos(st)|，而不维护具体的endpos(st)呢？就像我们在上周只维护了maxlen(st)和minlen(st)，而不维护具体的substrings(st)。

小Hi：你这个想法也很不错。可惜如果用上周的增量法建SAM时维护|endpos(st)|的话，额外的代价有点高。举个例子，假设我们已经建好了S="aaaaa"的SAM：

状态	子串	endpos	｜endpos｜
S	空串
1	a	{1,2,3,4,5,6}	5
2	aa	{2,3,4,5,6}	4
3	aaa	{3,4,5,6}	3
4	aaaa	{4,5,6}	2
5	aaaaa	{5,6}	1

当我们增加一个字符'a'，建立S="aaaaaa"的SAM：

状态	子串	endpos	｜endpos｜
S	空串
1	a	{1,2,3,4,5,6}	6
2	aa	{2,3,4,5,6}	5
3	aaa	{3,4,5,6}	4
4	aaaa	{4,5,6}	3
5	aaaaa	{5,6}	2
6	aaaaaa	{6}	1

你会发现前面的状态1-5都需要修改，它们的|endpos|都增加了1。

小Ho：所以我们如果维护|endpos(st)|的话，最坏情况下复杂度又会是O(length(S)^2)。那我们该怎么办呢？

小Hi：我们要换个思路，不追求在构造SAM的过程中同时把|endpos(st)|算出来。而是先构造SAM，再单独把每个状态的|endpos(st)|算一遍。还是以S="aabbabd"为例。

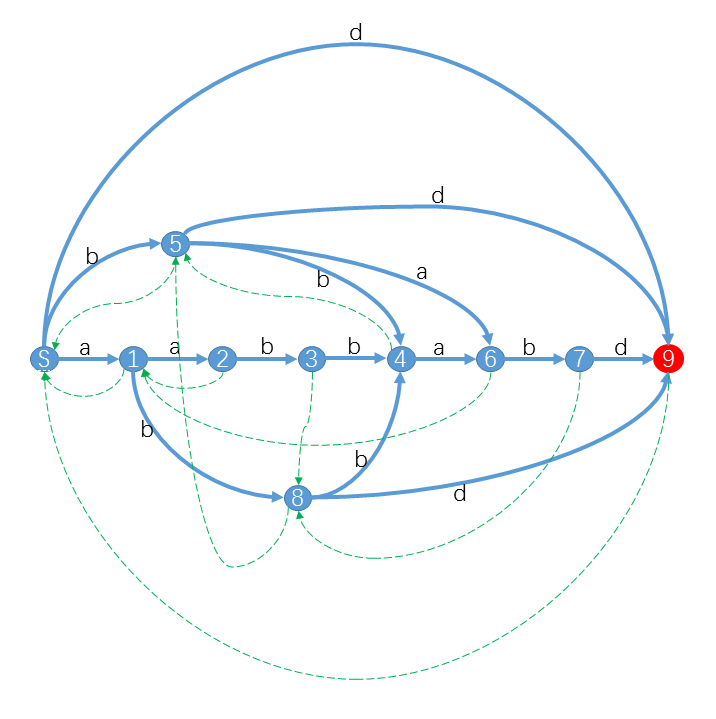
小Hi：这次我们不考虑Transition Function，只留下Suffix Links。此外，如果一个状态能接受（也就是包含）S的某个前缀的话，我们就把这个状态标记成绿色。例如状态4包含"aabb"，状态7包含"aabbab"。

状态	子串	endpos
S	空串	{0,1,2,3,4,5,6}
1	a	{1,2,5}
2	aa	{2}
3	aab	{3}
4	aabb,abb,bb	{4}
5	b	{3,4,6}
6	aabba,abba,bba,ba	{5}
7	aabbab,abbab,bbab,bab	{6}
8	ab	{3,6}
9	aabbabd,abbabd,bbabd,babd,abd,bd,d	{7}

小Hi：根据上上周基本概念中介绍的内容，我们知道Suffix Links把SAM中的所有状态连成了一棵树，并且父子(祖孙)之间的endpos集合有包含关系，非祖孙之间的endpos交集为空集。（还记得这个定理吗？对于S的两个子串s1和s2，不妨设length(s1) <= length(s2)，那么 s1是s2的后缀当且仅当endpos(s1) ⊇ endpos(s2)，s1不是s2的后缀当且仅当endpos(s1) ∩ endpos(s2) = ∅）。我们能不能"自底向上"求出所有状态的|endpos(st)|呢？

小Ho：好像有点意思。你继续讲。

小Hi：我们从2个具体的例子入手来分析这个问题。第一个例子是状态8，假设我们要求|endpos(8)|。我们知道状态8有两个儿子分别是状态3和状态7（即slink[7]=slink[3]=8)，其中endpos(3)={3}, endpos(7)={6}，这时|endpos(8)|是多少？

小Ho：看上去endpos(8)=endpos(3) ∪ endpos(7)。所以|endpos(8)| = |endpos(7)| + |endpos(3)|?

小Hi：我们再看一个例子，状态1，假设我们要求|endpos(1)|。我们知道状态1有两个儿子分别是状态2和状态6，其中endpos(2)={2}, endpos(6)={5}，这时|endpos(1)|是多少？

小Ho：endpos(1)是{1, 2, 5}，并不是endpos(2) ∪ endpos(6) = {2, 5}，多了一个元素1。

小Hi：通过这两个例子你有什么思路么？

小Ho：我们明白了。一个状态st对应的|endpos(st)|至少是它儿子的endpos大小之和。这一点还是比较容易证明的。假设x和y是st的两个儿子，那么根据Suffix Link的定义，我们知道st中的子串都是x中子串的后缀，也是y中子串的后缀。所以endpos(st) ⊇ endpos(x) 并且 endpos(st) ⊇ endpos(y)。又根据Suffix Link的定义我们知道x中的子串肯定不是y中子串的后缀，反之亦然，所以endpos(x) ∩ endpos(y) = ∅。所以|endpos(st)| >= |endpos(x)| + |endpos(y)|。

小Hi：那么|endpos(st)|可能比st儿子的endpos大小之和大多少呢？

小Ho：最多就大1。并且大1的情况当且仅当st是上文提到的绿色状态，即st包含S的某个前缀时才发生。我们分析endpos(1)={1, 2, 5}就会发现，它比endpos(2) ∪ endpos(6) = {2, 5}多出来的结束位置1的原因就是状态1还包含S的长度为1的前缀"a"。更一般的情形是如果某个状态st包含S的一个前缀S[1..l]，那么一定有l∈endpos(st)，并且l不能从st的儿子中继承过来。这时就需要+1。

小Hi：没错。那么我们如何判断哪些状态应该标记成绿色状态呢？

小Ho：可以在构造SAM的时候顺手做了。回顾我们构造SAM的算法，当新加入一个字符的时候，我们至少会新建一个状态z（还可能新建一个状态y），这个状态z一定是绿色状态（y一定不是）。

小Hi：没错，我们回顾一下。先构造SAM，顺手把绿色状态标记出来。然后再对Suffix Link连成的树"自底向上"求出每一个状态的|endpos(st)|，这一步"自底向上"可以通过拓扑排序完成，我们很早之前就讲过，不再赘述。

小Ho：求出每一个状态的|endpos(st)|后，我们还需要求出每个长度的子串最多出现了多少次。我对这一步还有疑问。假设ans[l]表示长度为l的子串最多出现的次数。我的想法是对于每个状态st，都要循环一遍，利用|endpos(st)|更新ans[minlen(st)] ... ans[maxlen(st)]的值。这一步复杂度好像又是O(length(S)^2)的，这不是功亏一篑了吗？我写的伪代码如下。

FOREACH State st:
FOR i = minlen(st) .. maxlen(st):
    ans[i] = max(ans[i], |endpos(st)|)

小Hi：你提的这个问题很好。这是我们最后要解决的一个问题了。值得注意的是ans[1], ans[2], ... ans[length(S)]一定是一个单调递减序列。所以我们对于每个状态st，只需要更新ans[maxlen(st)]。之后令i = length(S)-1 .. 1，从后向前扫描一遍，令ans[i] = max(ans[i], ans[i+1])，即可。伪代码如下，你仔细体会一下。

FOREACH State st:
    ans[maxlen(st)] = max(ans[maxlen(st)], |endpos(st)|)
FOR i = length(S) - 1 .. 1:
    ans[i] = max(ans[i], ans[i+1])

小Hi讲的实在太好了，就不说什么了。

 /*************************************************************************
     > File: main.cpp
     > Author: You Siki
     > Mail: You.Siki@outlook.com
     > Time: 2016年12月23日 星期五 15时14分18秒
  ************************************************************************/

 #include<bits/stdc++.h>

 //using namespace std;

 const int maxn = ;

 /* AUTOMATON */

 int last = ;
 int tail = ;
 int fail[maxn];
 int step[maxn];
 int flag[maxn];
 int next[maxn][];

 inline void buildAutomaton(char *s)
 {
     while (*s)
     {
         int p = last;
         int t = tail++;
         int c = *s++ - 'a';

         flag[t] = true;
         step[t] = step[p] + ;

         while (p && !next[p][c])
             next[p][c] = t, p = fail[p];

         if (p)
         {
             int q = next[p][c];
             if (step[q] == step[p] + )
                 fail[t] = q;
             else
             {
                 int k = tail++;
                 fail[k] = fail[q];
                 fail[q] = fail[t] = k;
                 step[k] = step[p] + ;
                 for (int i = ; i < ; ++i)
                     next[k][i] = next[q][i];
                 while (p && next[p][c] == q)
                     next[p][c] = k, p = fail[p];
             }
         }
         else
             fail[t] = ;
         last = t;
     }
 }

 int que[maxn];
 int cnt[maxn];
 int ans[maxn];

 inline int solveAndPrintAnswer(char *s)
 {
     int hd = , tl = , n = strlen(s);

     for (int i = ; i < tail; ++i)
         ++cnt[fail[i]];

     for (int i = ; i < tail; ++i)
         if (!cnt[i])que[tl++] = i;

     while (hd != tl)
     {
         int t = que[hd++];
         flag[fail[t]] += flag[t];
         if (--cnt[fail[t]] == )
             que[tl++] = fail[t];
     }

     for (int i = ; i < tail; ++i)
         if (ans[step[i]] < flag[i])
             ans[step[i]] = flag[i];

     for (int i = n; i; --i)
         if (ans[i] < ans[i + ])
             ans[i] = ans[i + ];

     for (int i = ; i <= n; ++i)
         printf("%d\n", ans[i]);
 }

 /* MAIN FUNC */

 char str[maxn];

 signed main(void)
 {
     scanf("%s", str);
     buildAutomaton(str);
     solveAndPrintAnswer(str);
 }

@Author: YouSiki