P9140 [THUPC 2023 初赛] 背包

prologue

这很难评（调了我 1h，我都想紫砂了。

还是典型得不重构就看不见系列。

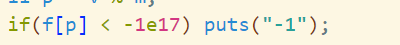
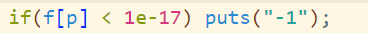
analysis

如果我们还是一个正常人，那么我们大体上是能看到题目的加粗字，这个格式很明显符合我们的同余最短路的格式。（如若不知，请先出门直走）

然后我们就要考虑这个同余最短路的实现。这个题目不同于往常的同余最短路，而是新增了一个条件。除了显然得他是给到完全背包，我们决定用同余最短路解决之后，我们该考虑怎么让他这个完全背包利益最大化。

（不知道你们有没有，反正我学 01背包的时候是先教的我用单位价值进行排序然后一个一个加。）

我们就可以借助上述的贪心，先找到单位体积最大的即 \(\frac{c_i}{v_i}\)，这个很好实现，即在实现输入的时候发现 \(\frac{c_i}{v_i} > \frac{w}{m}\)，更新\(m\)、\(w\)即可，为了规避整数除法，我们将式子转换成 \(c_i \times m > w \times a_i\)就可以实现维护。

之后就是我们进行同余最短路的时候。

附上一句：同余最短路写最短路就好比打游戏玩原神。

下面不讲常规方法，讲的是转圈做法。（都 3202 年了你还不会转圈？那就赶紧左转或者右转到大佬的博客进行学习。）

之后是统计答案。（下面的过程参考了大佬的这篇博客，想看原汁原味的可以去这位大佬的博客中查看）

令 \(v \gets V \bmod m, v < V\)，这个时候我们将考虑到最终最大值为 \(C + \frac{V - v}{m} \times w\)，也就是我们要求 \(C - \frac{v}{m} \times w\) 最大。也就得到我们的转移方程：

\[f_p \gets f_t + c[i] - ((t + a[i]) / m) \times w, t = p
\]

我们在查询答案的时候，如果这个位置的 f 值不为 \(-∞\) 就得到：

\[ans \gets f[p] + \frac{v}{m} \times w
\]

code time

马蜂优良。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define rl register ll

constexpr ll N = 55, M = 1e5 +10;

ll n, m = 1, q, a[N], f[M], c[N], ans, w;

inline ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }

int main()
{
    // freopen("1.in", "r", stdin), freopen("1.out", "w", stdout);

    cin >> n >> q;

    for(rl i=1; i <= n; ++ i)
    {
        cin >> a[i] >> c[i];
        if(w * a[i] < m * c[i]) w = c[i], m = a[i];
    }

    for(rl i=1; i < m; ++ i) f[i] = -1e18;
    for(rl i=1; i <= n; ++ i)
        for(rl j=0, lim = gcd(m, a[i]); j < lim; ++ j)
            for(rl t = j, asd = 0; asd < 2; asd += t == j)
            {
                ll p = (t + a[i]) % m;
                f[p] = max(f[p], f[t] + c[i] - ((t + a[i]) / m) * w), t = p;
            }

    while(q -- )
    {
        ll v; cin >> v;
        ll p = v % m;
        if(f[p] < -1e17) puts("-1");
        else cout << f[p] + v / m * w << endl;
    }
    return 0;
}