浅谈舞蹈链（DLX）

名字：

\(DL\)，\(Dancing\space Link\)，舞蹈链，是由\(Donald\space Knuth\)提出的数据结构，用来优化 \(X\) 算法，所以叫\(DLX\)

\(X\)算法详解

用于求解精确覆盖问题，精确覆盖问题的定义：给定一个由0-1组成的矩阵，是否能找到一个行的集合，使得集合中每一列都恰好包含一个1

例：

若\(A,B,C \subseteq S\)

\(A \space \cap \space B= Ø\)，\(A \space \cup \space B=S\)，则集合\(A,B\)是问题的一种解

\(X\)算法求解模拟：

给出矩阵\(A\)

\[A=\left(
\begin{matrix}
0&0&1&0&1&1&0\\1&0&0&1&0&0&1\\0&1&1&0&0&1&0\\1&0&0&1&0&0&0\\0&1&0&0&0&0&1\\0&0&0&1&1&0&1
\end{matrix}
\right)
\]

选择第一列：

\[\left(
\begin{matrix}
0&0&1&0&1&1&0\\\\\\\\\\
\end{matrix}
\right)
\]

将有\(1\)的列向下延伸，若该行有\(1\)，标记该行，处理\(A\)矩阵，得到\(B\)矩阵

\[B=\left(
\begin{matrix}
0&0&1&0&1&1&0\\&&0&&0&0\\0&1&1&0&0&1&0\\&&0&&0&0\\&&0&&0&0\\0&0&0&1&1&0&1
\end{matrix}
\right)
\]

\(S矩阵=A矩阵-B矩阵\)（删除所标记的行和列）

\[A_1=\left(
\begin{matrix}
1&0&1&1\\1&0&1&0\\0&1&0&1
\end{matrix}
\right)
\]

再选择第一列

\[\left(
\begin{matrix}
1&0&1&1\\\\\\
\end{matrix}
\right)
\]

标记

\[B_1=
\left(
\begin{matrix}
1&0&1&1\\1&&1&0\\0&1&0&1
\end{matrix}
\right)
\]

得到新矩阵,又得到一个规模较小的精确覆盖问题

\[S_1=
\left(
\begin{matrix}
0
\end{matrix}
\right)
\]

发现\(A\)矩阵不是空的，也没有一列有\(1\)（无法继续操作）

回溯

\[A_1=\left(
\begin{matrix}
1&0&1&1\\1&0&1&0\\0&1&0&1
\end{matrix}
\right)
\]

不能尝试第一行，标记第二行，尝试继续拓展

\[B_2=
\left(
\begin{matrix}
1&0&1&1\\1&0&1&0\\0&&0
\end{matrix}
\right)
\]

同理可得

\[A_3=
\left(
\begin{matrix}
1&1
\end{matrix}
\right)
\]

\(A_3\)中只有\(1\)行，且都是\(1\)，选择这行，问题就可以解决

故，问题的解就是矩阵\(A\)中的第一行、矩阵\(A_1\)中的第\(2\)行、矩阵\(A_3\)的第一行，即矩阵\(A\)中的第\(1、4、5\)行

言归正传，DLX又是什么东西呢

介绍DL，舞蹈链

建出形如这样的交叉十字循环双向链，只对有\(1\)的连边，这张图对应着矩阵\(A\)

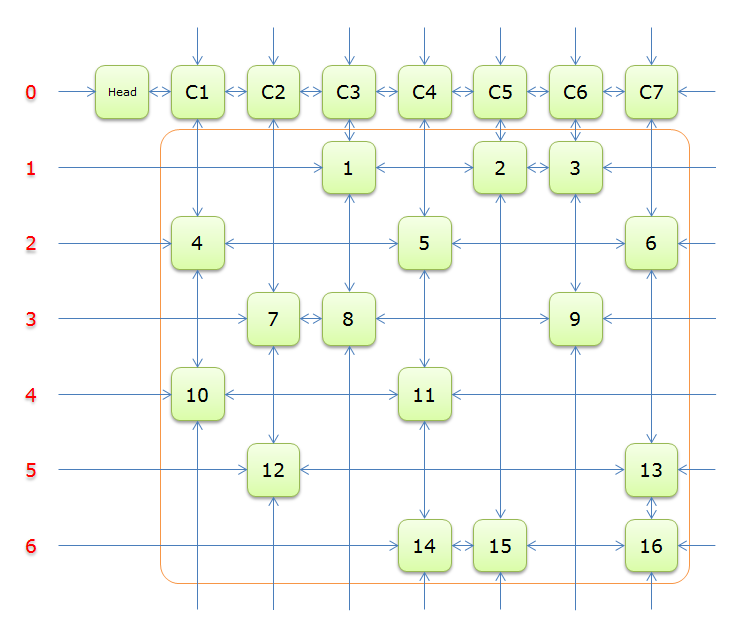
获取\(head.right\)元素，即元素\(C1\)，标示元素\(C1\)为紫色

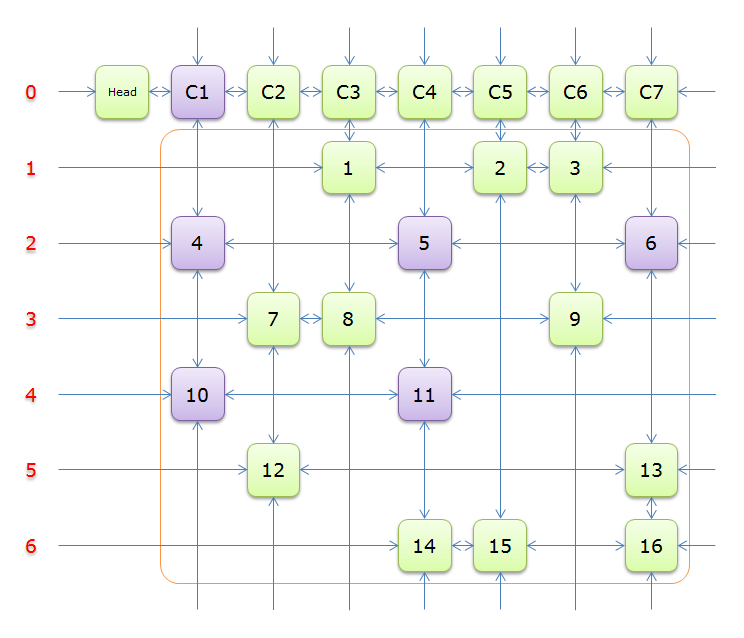
先尝试行\(2\)，标示该行中其他元素\(元素5和元素6\)所在的列首元素为橙色，即元素\(C4\)和元素\(C7\)

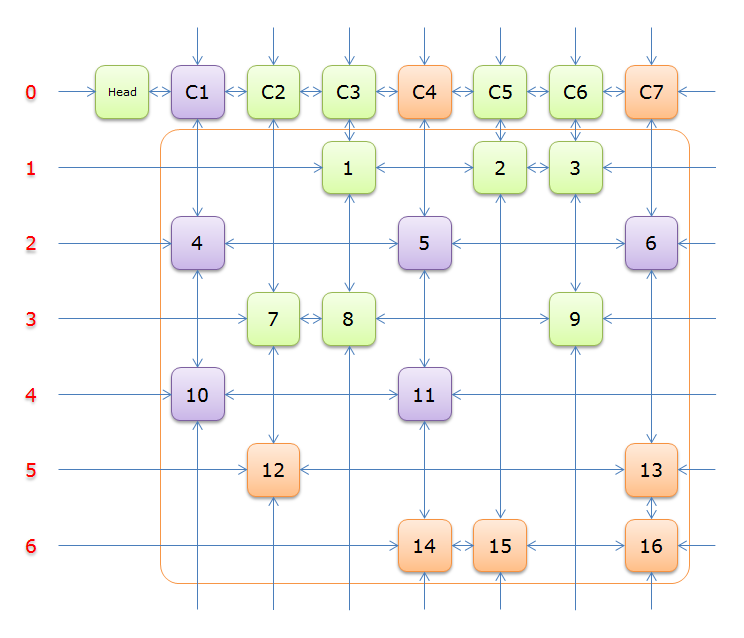
移除橙色部分和紫色部分，剩下的如图所示

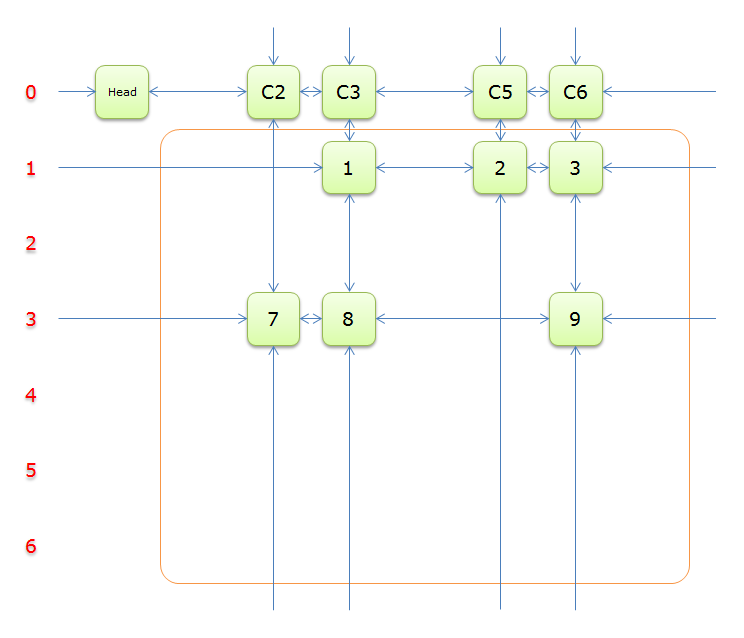
获取\(head.right\)元素，即元素\(C2\)，标示元素\(C2\)为紫色

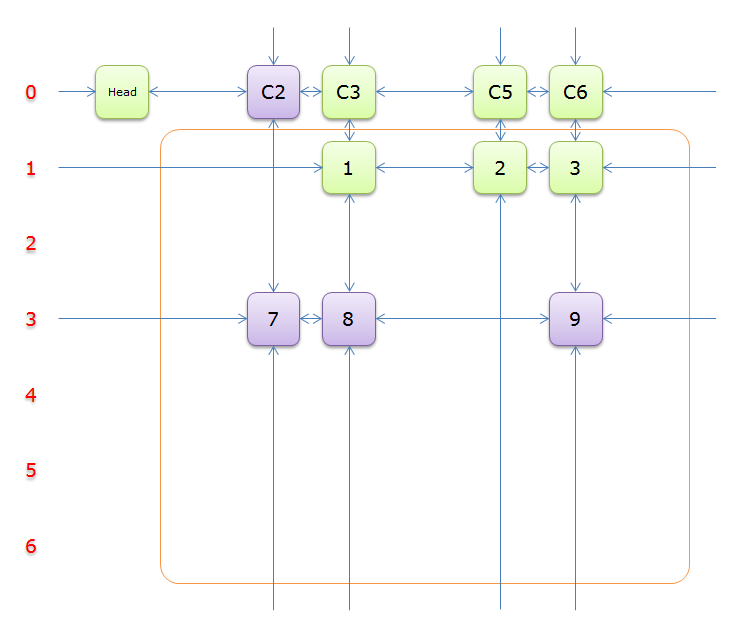
列\(C2\)只有元素\(7\)覆盖，故答案只能选择行\(3\)

选择行\(3\)，同理，标示元素\(C3\)和标示元素\(C6\)为橙色

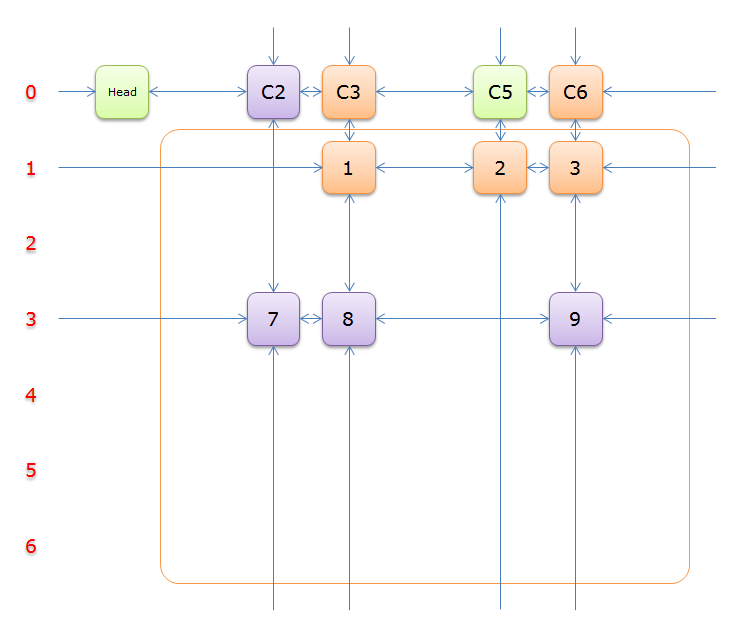
移除，得

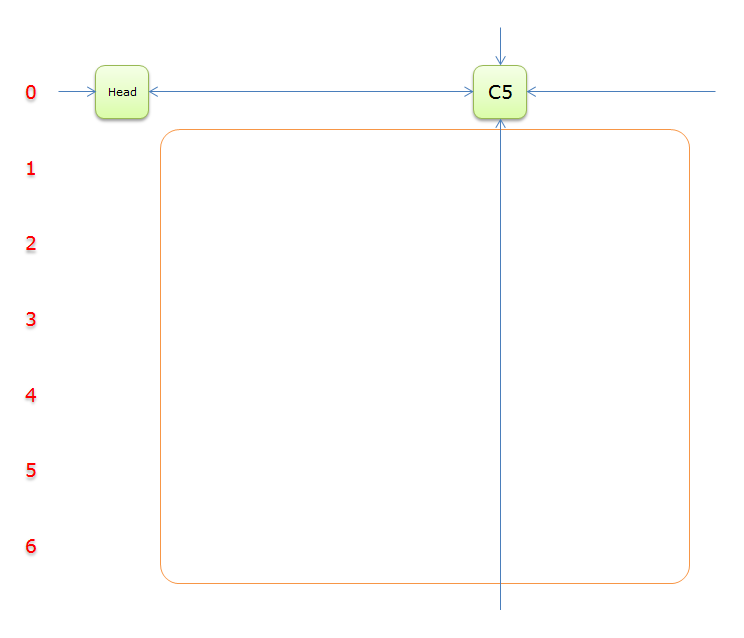
没有元素能覆盖到\(C5\)，说明求解失败，回溯

回标列首元素，其顺序是标示元素的顺序反过来，即回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4

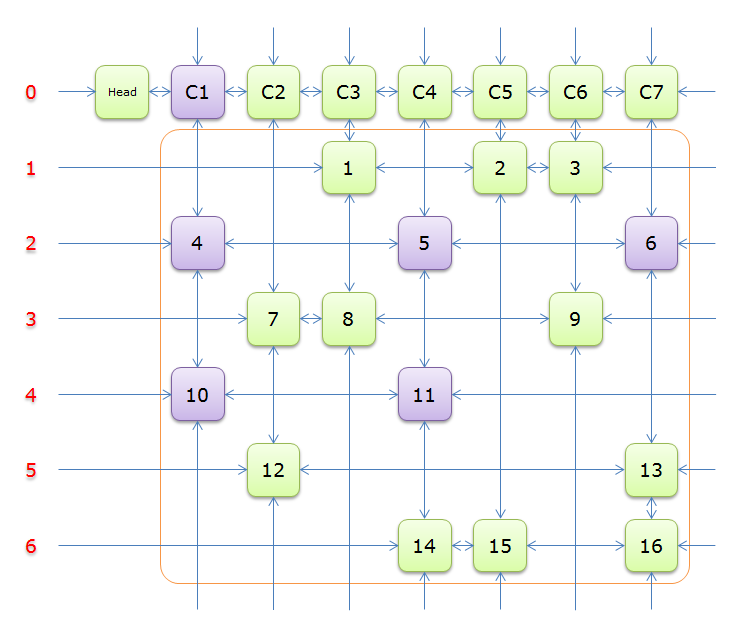
故不能选择行\(2\)，尝试行\(4\)，同理，标示元素\(C4\)为橙色

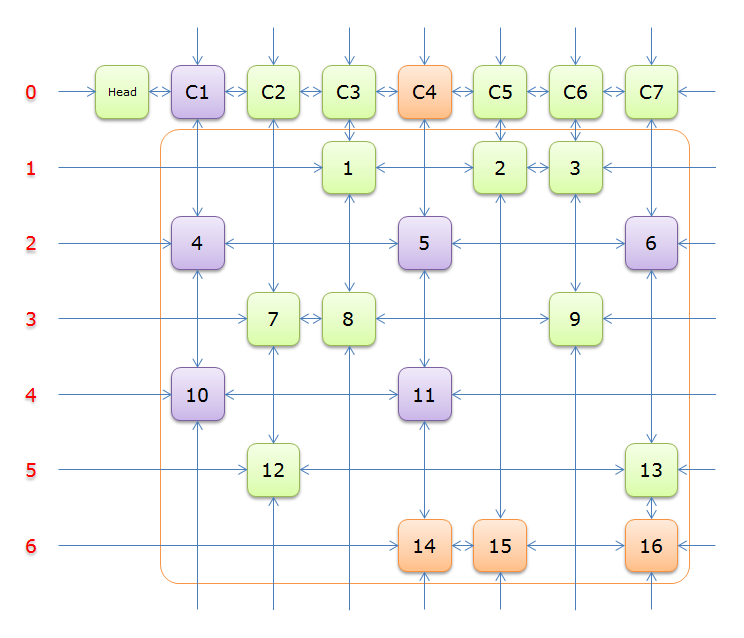
移除，得

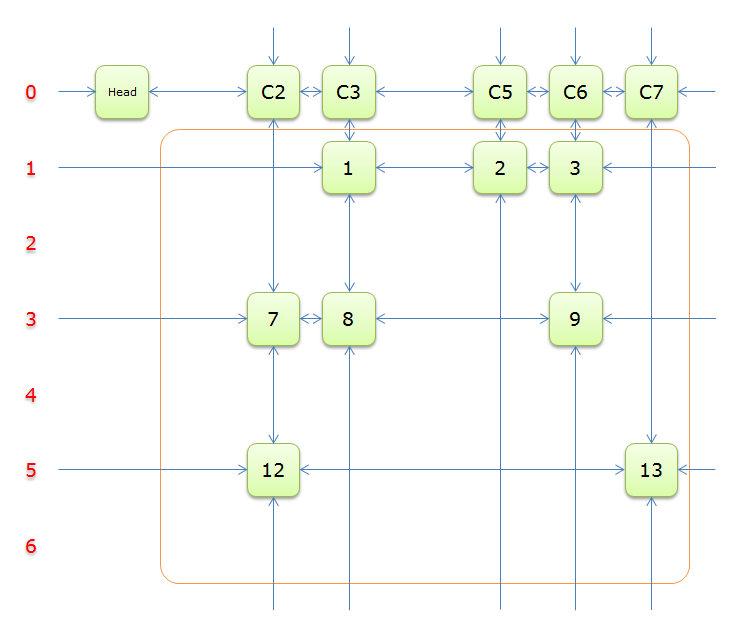
获取\(head.right\)元素，标示元素\(C2\)为紫色

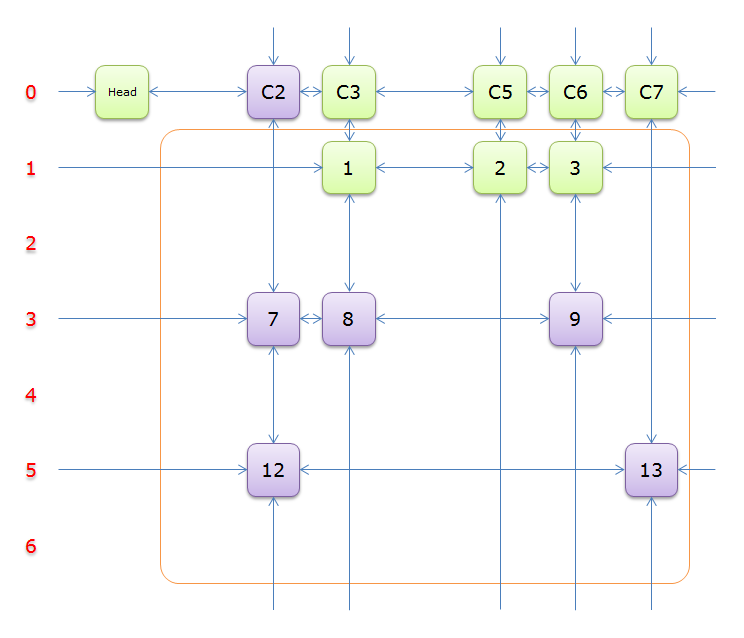
选择行\(3\)，同理，标示元素\(C3\)和\(C6\)为橙色

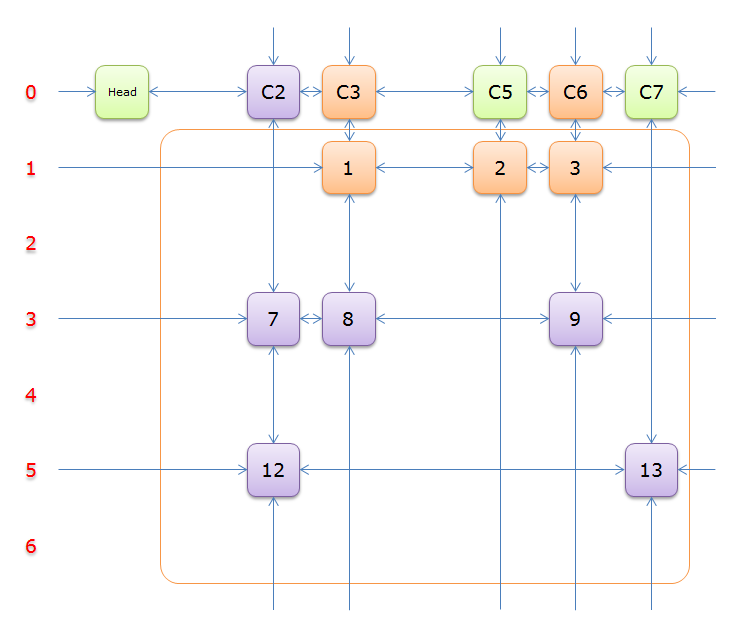
同理，得

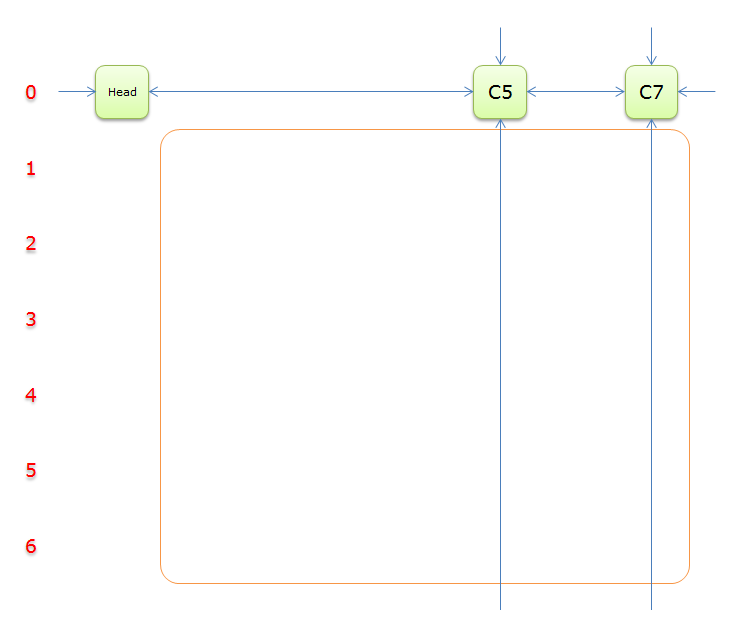
同理，回溯，回标列首C6、回标列首C3

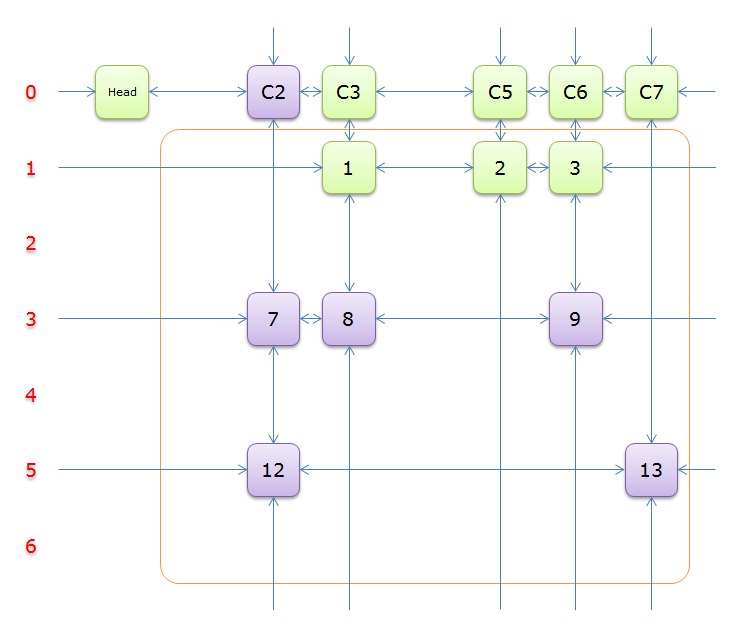
这次选择行\(5\)，标示元素\(C7\)为橙色

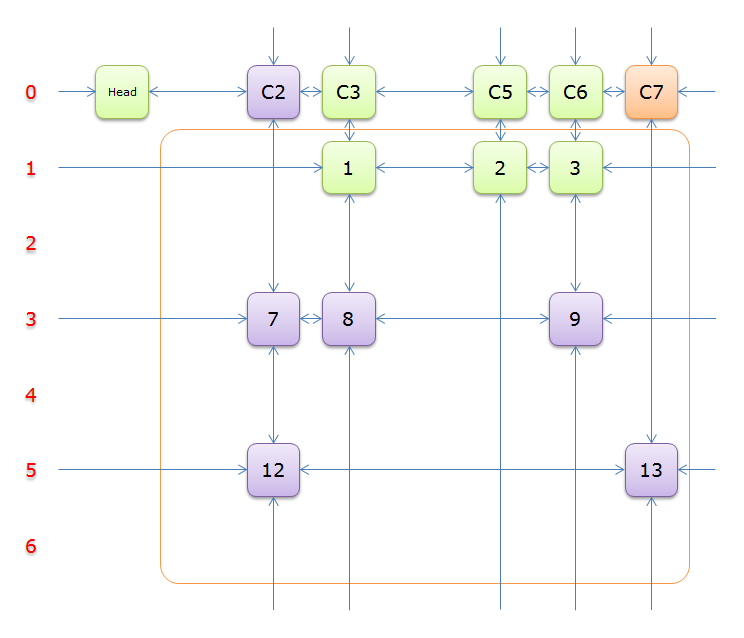
移除，得

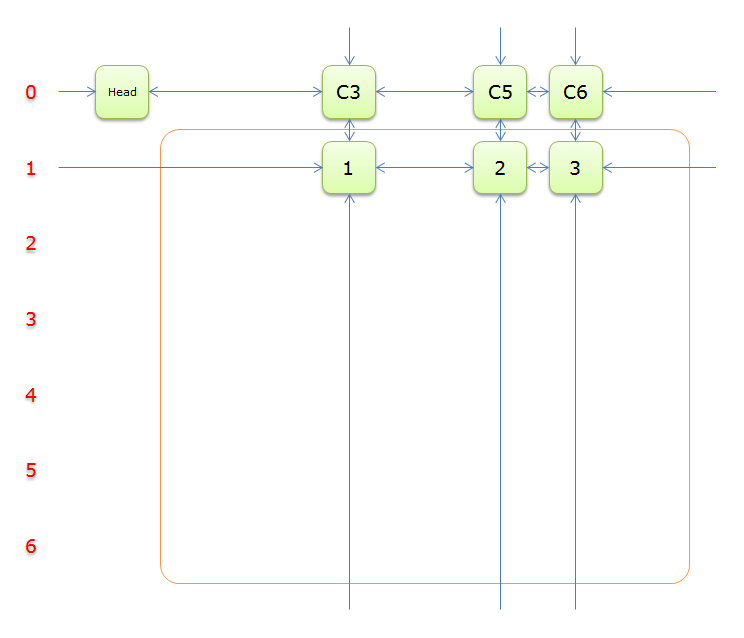
获取\(head.right\)元素，标示元素\(C3\)为紫色

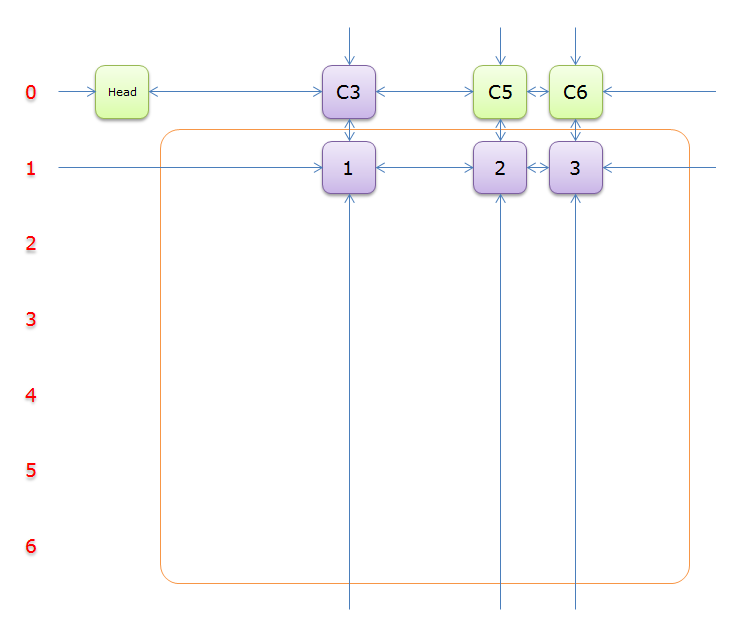
只有元素\(1\)覆盖，故答案只能选择行\(3\)，同理，标示元素\(C5\)和元素\(C6\)为橙色

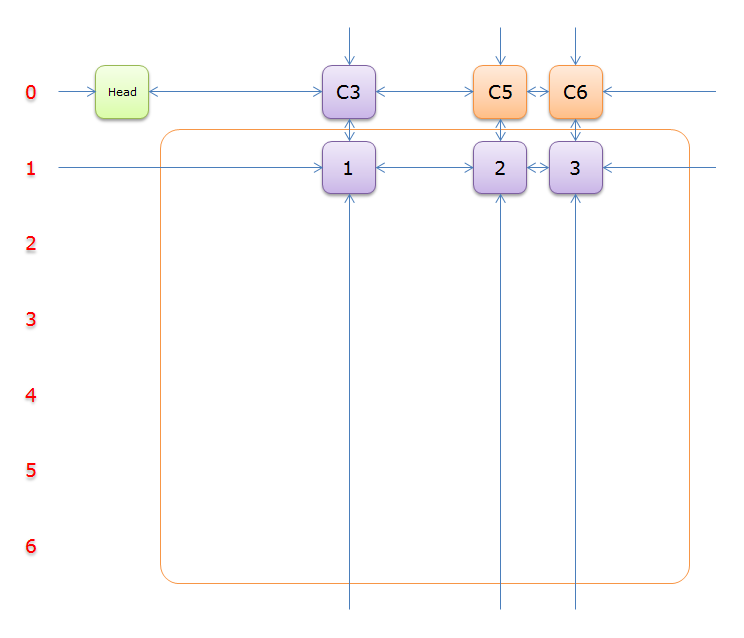
移除，得

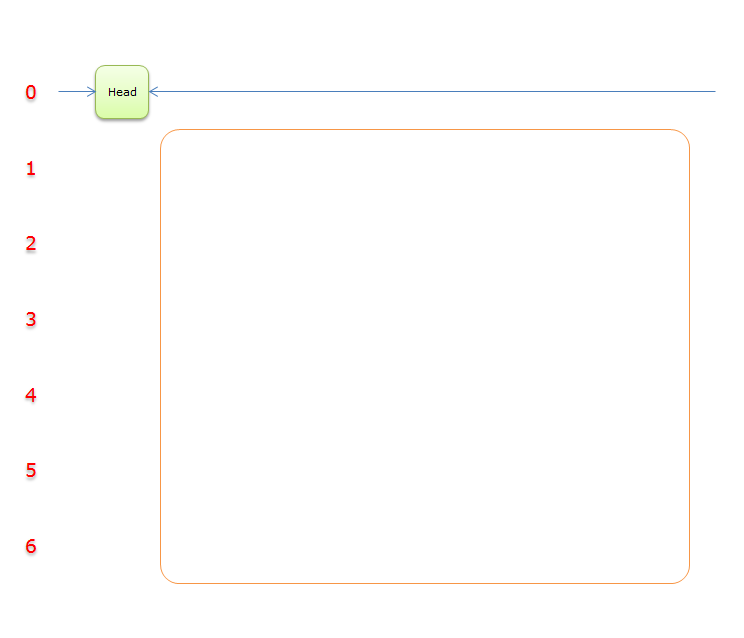
因为\(head.right=head\)，故求解结束，答案栈中的答案分别是\(4、5、1\)，表示该问题的解是第\(4、5、1\)行覆盖所有的列，即下图蓝色的部分

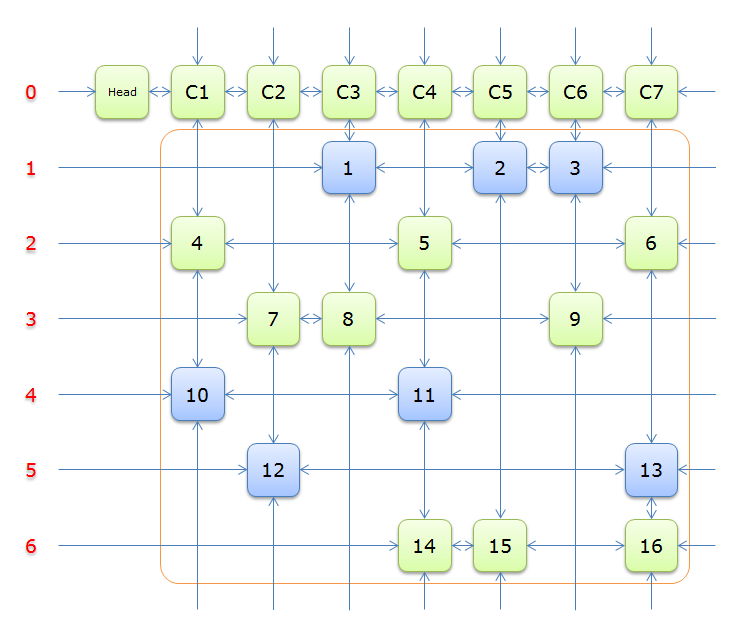
总结\(Dancing Links\)的求解

• 函数入口
• 判断$head.right \space ?= head $，若成立，输出答案，返回已解决，退出函数
• 获得\(head.right\)的元素\(C\)
• 标示元素\(C\)
• 获得元素\(C\)所在列的一个元素
• 标示该元素同行的其他元素所在的列首元素
• 获得一个简化问题，递归，若返回已解决，则退出函数
• 若刚刚尝试的不行，回标该元素同行的其他元素所在的列首元素，回标顺序与之前标示的顺序相反
• 获得元素\(C\)所在列的下一个元素，若有，跳转“标示该元素同行的其他元素所在的列首元素”
• 若没有，回标元素\(C\)，返回未解决，退出函数

例题 P4929

代码实现

#include"bits/stdc++.h"
using namespace std;
const int N=250015;//N*M
#define inl inline
#define reg register
#define regi register int
#define PII pair<int,int>
inl int read(void)
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch))  f=ch=='-'?-1:f,ch=getchar();
	while(isdigit(ch))   x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
	return x*f;
}
int l[N],r[N],up[N],down[N],col[N],row[N];//每个点的左右上下指针，以及每个点所在的行列
int head[N];int sz[N];//每行的头结点,每列的节点数
int ans[N];//答案栈
int n,m,cnt;
void build(int m)
{
	for(int i=0;i<=m;i++)	r[i]=i+1,l[i]=i-1,up[i]=down[i]=i;
	r[m]=0,l[0]=m;
	memset(sz,0,sizeof sz);
	cnt=m+1;//已经处理了0行，从第一行开始insert
}
void insert(int R,int C)//在R行C列插入点
{
	sz[C]++;
	row[++cnt]=R,col[cnt]=C;
	up[cnt]=C,down[cnt]=down[C];
	up[down[C]]=cnt,down[C]=cnt;
	if(!head[R])	head[R]=r[cnt]=l[cnt]=cnt;
	else	r[cnt]=head[R],l[cnt]=l[head[R]],r[l[head[R]]]=cnt,l[head[R]]=cnt;
}
void remove(int C)//删除C列的集合
{
	r[l[C]]=r[C],l[r[C]]=l[C];
	for(int i=down[C];i!=C;i=down[i])
		for(int j=r[i];j!=i;j=r[j])
			up[down[j]]=up[j],down[up[j]]=down[j],sz[col[j]]--;
}
void resume(int C)//恢复C列的集合
{
	for(int i=up[C];i!=C;i=up[i])
		for(int j=l[i];j!=i;j=l[j])
			up[down[j]]=down[up[j]]=j,sz[col[j]]++;
	r[l[C]]=C,l[r[C]]=C;
}
bool dance(int dep)
{
	if(r[0]==0)//head.right=head
	{
		for(int i=0;i<dep;i++)	printf("%d ",ans[i]);
		return 1;
	}
	int C=r[0];
	for(int i=r[0];i;i=r[i])	if(sz[i]<sz[C])	C=i;//找到点最少的列（优化）
	remove(C);
	for(int i=down[C];i!=C;i=down[i])
	{
		ans[dep]=row[i];//压入答案栈
		for(int j=r[i];j!=i;j=r[j])	remove(col[j]);
		if(dance(dep+1))	return 1;
		for(int j=l[i];j!=i;j=l[j])	resume(col[j]);
	}
	resume(C);
	return 0;
}
int main(void)
{
	n=read(),m=read();
	int s;
	build(m);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			s=read();
			if(s)	insert(i,j);
		}
	if(!dance(0))	puts("No Solution!");//无解
	return 0;
}