minIO系列文章01---MinIO 简介

MinIO.jpeg

1、什么是对象存储？

关于对象存储，我们可以看下阿里云OSS 的解释。

对象存储服务OSS（Object Storage Service）是一种海量、安全、低成本、高可靠的云存储服务，适合存放任意类型的文件。容量和处理能力弹性扩展，多种存储类型供选择，全面优化存储成本。

对象存储最大的优势就在于它可以存储大容量的非结构化数据，例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等。对于大多数的企业来说，这可以说是最为理想的存储媒介了。

对于业务已在公有云上的企业来说，使用公有云提供的 OSS 服务，可以很好的节省存储的成本，且一般都提供易接入的 SDK，以阿里云的OSS 服务为例，在存储介质的上层封装可标注的 RESTful API 接口，使用起来十分方便。

但是对于一些没有选择业务上云或者想要下云的企业来说，要使用公有云的 OSS，在公网带宽方面就需要有一定的投入，毕竟需要通过公网传输，带宽太小，传输速度就会慢，且在传输过程中数据的安全性和完整性也有损失的风险，走专线的费用又十分昂贵，不实在。

这种情况下，MinIO 就是一个不错的选择，麻雀虽小，五脏俱全，企业可以以此快速构建自己内部的对象存储服务。

2、什么是 MinIO？

Minio 是个基于 Golang 编写的开源对象存储套件，基于Apache License v2.0开源协议，虽然轻量，却拥有着不错的性能。它兼容亚马逊S3云存储服务接口。可以很简单的和其他应用结合使用，例如 NodeJS、Redis、MySQL等。

1）MinIO 的应用场景

如下图，MinIO 的应用场景除了可以作为私有云的对象存储服务来使用，也可以作为云对象存储的网关层，无缝对接 Amazon S3 或者 MicroSoft Azure 。

MinIO 应用场景.png

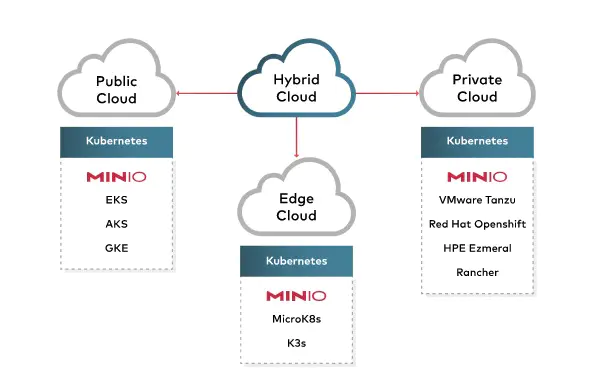
2）特点

高性能:

作为一款高性能存储，在标准硬件条件下，其读写速率分别可以达到 55Gb/s 和 35Gb/s。并而 MinIO 支持一个对象文件可以是任意大小，从几kb到最大5T不等。
可扩展:

不同MinIO集群可以组成联邦，并形成一个全局的命名空间，并且支持跨越多个数据中心。
云原生:

容器化、基于K8S的编排、多租户支持。
Amazon S3兼容:

使用 Amazon S3 v2 / v4 API。可以使用Minio SDK，Minio Client，AWS SDK 和 AWS CLI 访问Minio服务器。
可对接多种后端存储:

除了Minio自己的文件系统，还支持 DAS、 JBODs、NAS、Google云存储和 Azure Blob存储。
SDK支持:
- GO SDK： https://github.com/minio/minio-go
- JavaSDK： https://github.com/minio/minio-java
- PythonSDK： https://github.com/minio/minio-py
Lambda计算:

Minio服务器通过其兼容AWS SNS / SQS的事件通知服务触发Lambda功能。支持的目标是消息队列，如Kafka，NATS，AMQP，MQTT，Webhooks以及Elasticsearch，Redis，Postgres和MySQL等数据库。
图形化界面

有操作页面。
功能简单:

不容易出错，快速启动。
支持纠删码:

MinIO使用纠删码、Checksum来防止硬件错误和静默数据污染。在最高冗余度配置下，即使丢失1/2的磁盘也能恢复数据。

3）存储机制

Minio 使用纠删码 erasure code和校验和 checksum。即便丢失一半数量（N/2）的硬盘，仍然可以恢复数据。

校验和

保护数据免受硬件故障和无声数据损坏

纠删码

纠删码是一种恢复丢失和损坏数据的数学算法，目前，纠删码技术在分布式存储系统中的应用主要有三类，阵列纠删码（Array Code: RAID5、RAID6等）、RS(Reed-Solomon)里德-所罗门类纠删码和LDPC(LowDensity Parity Check Code)低密度奇偶校验纠删码。Erasure Code是一种编码技术，它可以将n份原始数据，增加m份数据，并能通过n+m份中的任意n份数据，还原为原始数据。即如果有任意小于等于m份的数据失效，仍然能通过剩下的数据还原出来。

Minio采用Reed-Solomon code将对象拆分成N/2数据和N/2 奇偶校验块。这就意味着如果是12块盘，一个对象会被分成6个数据块、6个奇偶校验块，可以丢失任意6块盘（不管其是存放的数据块还是奇偶校验块），仍可以从剩下的盘中的数据进行恢复。

RS code编码数据恢复原理

RS编码以word为编码和解码单位，大的数据块拆分到字长为w（取值一般为8或者16位）的word，然后对word进行编解码。数据块的编码原理与word编码原理相同，后文中以word为例说明，变量Di, Ci将代表一个word。

把输入数据视为向量D=(D1，D2，..., Dn）, 编码后数据视为向量（D1, D2,..., Dn, C1, C2,.., Cm)，RS编码可视为如下（图1）所示矩阵运算。

图1最左边是编码矩阵（或称为生成矩阵、分布矩阵，Distribution Matrix），编码矩阵需要满足任意n*n子矩阵可逆。为方便数据存储，编码矩阵上部是单位阵（n行n列），下部是m行n列矩阵。下部矩阵可以选择范德蒙德矩阵或柯西矩阵。

minio 存储机制1.png

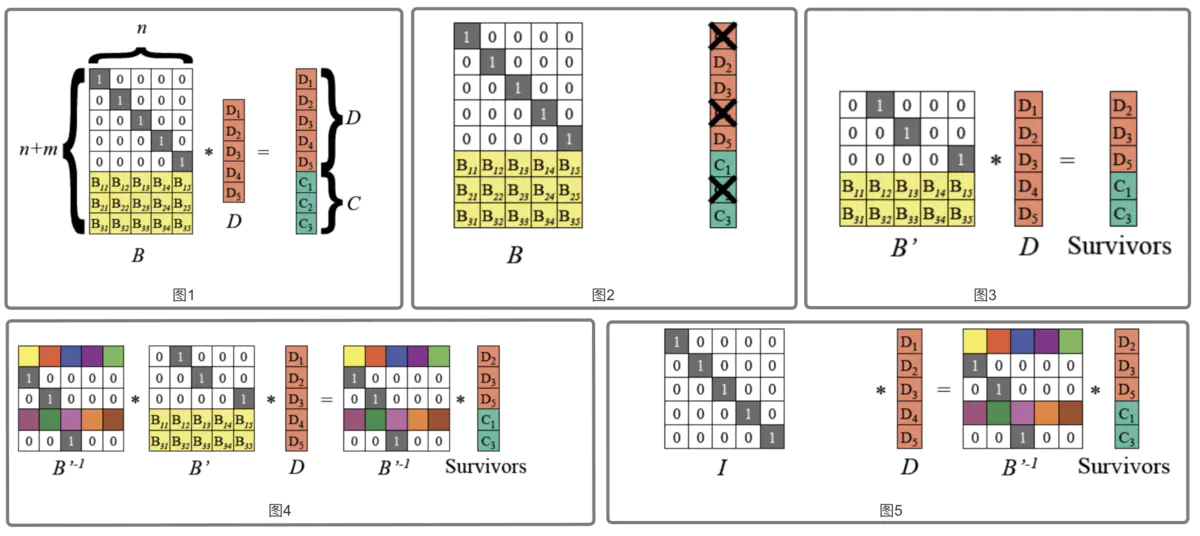
RS最多能容忍m个数据块被删除。数据恢复的过程如下：

（1）假设D1、D4、C2丢失，从编码矩阵中删掉丢失的数据块/编码块对应的行。（图2、3）

（2）由于B' 是可逆的，记B'的逆矩阵为 (B'^-1)，则B' * (B'^-1) = I 单位矩阵。两边左乘B' 逆矩阵。（图4、5）

（3）得到如下原始数据D的计算公式。

minio 存储机制2.png

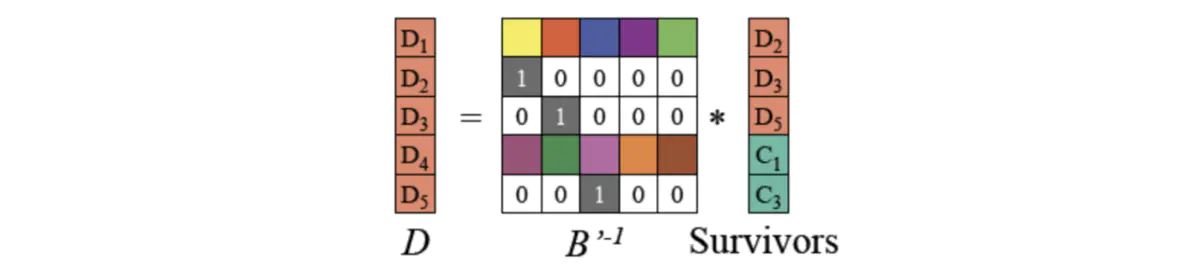
（4）对D重新编码，可得到丢失的编码

参考文档:

https://www.jianshu.com/p/c2b43ff67df0

作者：独奏乱序
链接：https://www.jianshu.com/p/f39e7255805b
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。