Special Prime

Special Prime

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 415    Accepted Submission(s): 220

Problem Description

Give
you a prime number p, if you could find some natural number (0 is not
inclusive) n and m, satisfy the following expression:
  
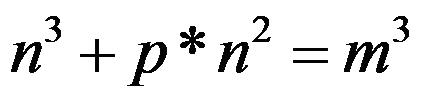
We call this p a “Special Prime”.
AekdyCoin want you to tell him the number of the “Special Prime” that no larger than L.
For example:
  If L =20
1^3 + 7*1^2 = 2^3
8^3 + 19*8^2 = 12^3
That is to say the prime number 7, 19 are two “Special Primes”.

 

Input

The input consists of several test cases.
Every case has only one integer indicating L.(1<=L<=10^6)

 

Output

For each case, you should output a single line indicate the number of
“Special Prime” that no larger than L. If you can’t find such “Special
Prime”, just output “No Special Prime!”

 

Sample Input

7

777

Sample Output

1

10

思路：假设 n^2 和 n+p 之间有公共素因子 p , 那么 n+p = k*p , 即 n=p*（k-1）,带进去得到 p^3 * (k-1)^2 *k = m^3 , (k-1)^2*k 肯定是不能表示成某一个数的三次幂的，所以假设不成立,gcd(K,K+1)=1,假设n=x^3 , n+p=y^3 , 相减得到 p = y^3 - x^3 = (y-x) *(y^2+y*x+x^2)p是素数，y-x=1 ， p =(x+1)^3 - x^3 = 3*x^2+3*x+1,然后枚举x，判断求得数是否是素数即可；

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<queue>
 5 #include<set>
 6 #include<math.h>
 7 #include<string.h>
 8 using namespace std;
 9 typedef long long LL;
10 bool prime[1000005];
11 int sum[1000005];
12 int main(void)
13 {
14         int i,j;
15         memset(sum,0,sizeof(sum));
16         for(i = 2; i <=1000; i++)
17         {
18                 if(!prime[i])
19                 {
20                         for(j = i; (i*j) <= 1000000; j++)
21                         {
22                                 prime[i*j] = true;
23                         }
24                 }
25         }
26         for(i = 0;; i++)
27         {
28                 int x = 3*i*i+3*i+1;
29                 if(x > 1e6)
30                         break;
31                 if(!prime[x])
32                 {
33                         sum[x] = 1;
34                 }
35         }sum[1] = 0;
36         for(i = 1; i <= 1e6; i++)
37         {
38                 sum[i] += sum[i-1];
39         }
40         int n;
41         while(scanf("%d",&n)!=EOF)
42         {       if(sum[n])
43                 printf("%d\n",sum[n]);
44                 else printf("No Special Prime!\n");
45         }
46         return 0;
47 }