Codeforces 1015E1 Stars Drawing (Easy Edition)
题面:


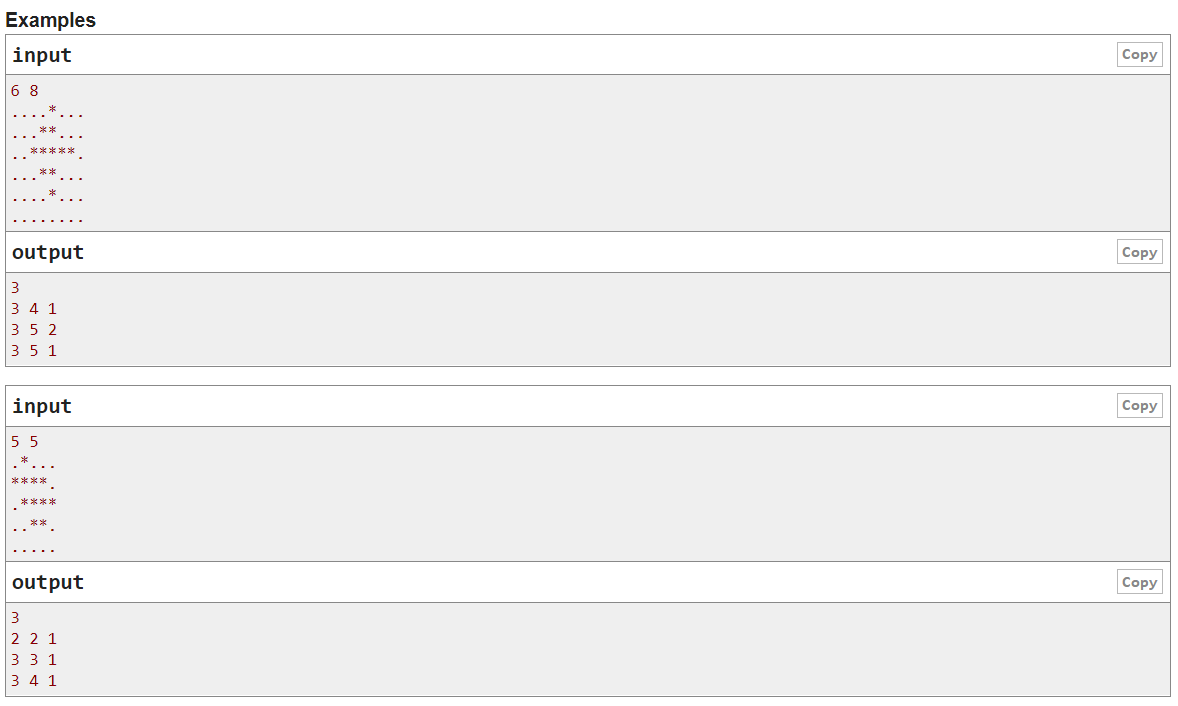
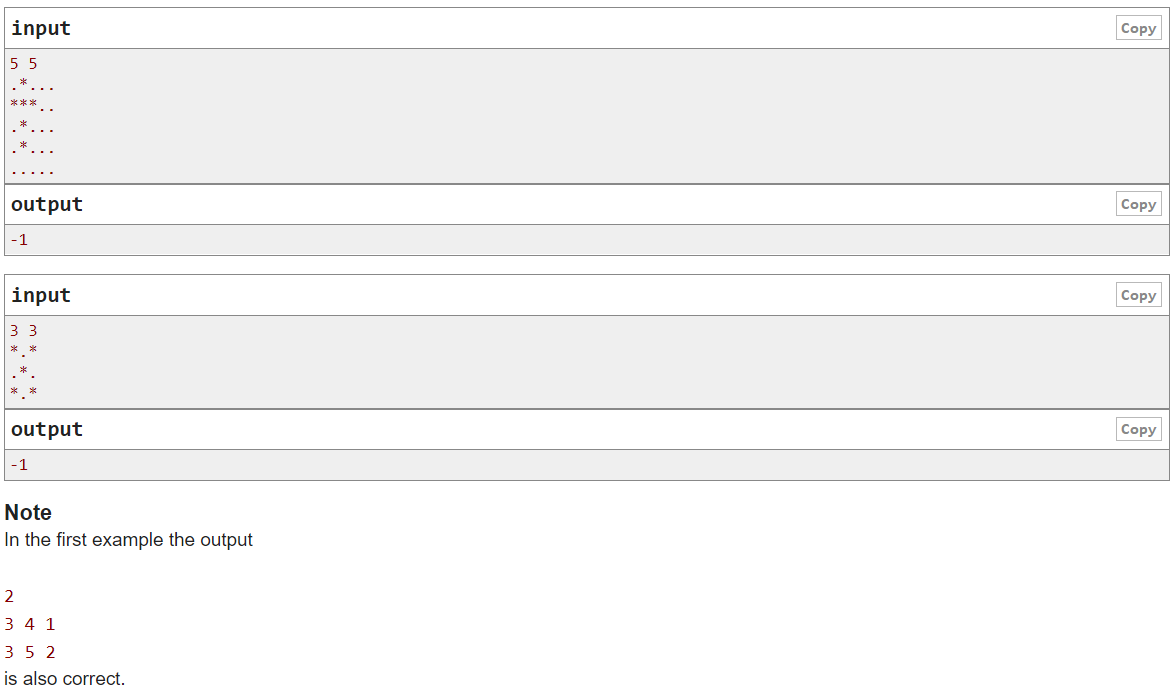
题目描述:
题目分析:





1 #include <iostream>
2 #include <cstdio>
3 #include <cstring>
4 #include <algorithm>
5 #include <stack>
6 #include <queue>
7 using namespace std;
8 const int maxn = 105;
9 char a[maxn][maxn]; //原星图
10 int point[maxn][maxn]; //自己画的图
11 int dr[4] = {-1, 1, 0, 0}, dc[4] = {0,0,-1,1}; //上下左右
12 int n, m;
13
14 struct node{
15 int x;
16 int y;
17 int type;
18 };
19
20 queue<node> q; //用队列保存结果
21
22 int check(int r, int c){ //检查是否能画
23 int flag;
24 int r1, c1;
25 node temp;
26 temp.type = 0;
27 for(int sizes = 1; sizes <= 50; sizes++){
28 flag = 1;
29 for(int i = 0; i < 4; i++){
30 r1 = r + dr[i]*sizes;
31 c1 = c + dc[i]*sizes;
32 if(r1 >= 0 || r1 < n || c1 >= 0 || c1 < m){
33 if(a[r1][c1] != '*') flag = 0; //如果上下左右不是星号就不能画
34 }
35 else {flag = 0; break;}
36 }
37
38 if(flag){ //保存能画的最大十字星星
39 point[r][c] = 1;
40 for(int i = 0; i < 4; i++){
41 r1 = r + dr[i]*sizes;
42 c1 = c + dc[i]*sizes;
43 point[r1][c1] = 1;
44 }
45 temp.type = sizes;
46 temp.x = r;
47 temp.y = c;
48 }
49 else break;
50 }
51 if(temp.type) {q.push(temp);return 1;} //把结果加入队列
52 return 0;
53 }
54
55 bool check2(){ //检查画出来的是否和原星图一致
56 for(int i = 0; i < n; i++){
57 for(int j = 0; j < m; j++){
58 if(a[i][j] == '*'){
59 if(point[i][j]==0) return false;
60 }
61 }
62 }
63 return true;
64 }
65
66 int main(){
67 memset(a, 0, sizeof(a));
68 memset(point, 0, sizeof(point));
69 cin >> n >> m;
70 for(int i = 0; i < n; i++) cin >> a[i];
71
72 int cnt = 0; //计数
73 node temp;
74 for(int i = 0; i < n; i++){
75 for(int j = 0; j < m; j++){
76 if(a[i][j] == '*'){
77 if(check(i, j)){ //符合条件就画
78 cnt++;
79 }
80 }
81 }
82 }
83
84 if(check2()){
85 printf("%d\n", cnt);
86 while(!q.empty()){
87 temp = q.front(); q.pop();
88 printf("%d %d %d\n", temp.x+1, temp.y+1, temp.type);
89 }
90 }
91 else cout << -1 << endl;
92 return 0;
93 }
Codeforces 1015E1 Stars Drawing (Easy Edition)的更多相关文章
- CF 。E2. Stars Drawing (Hard Edition) (DP)
Description: 定义一个星星由 '*' 组成,形状为一个对称的“十”字型,大小为星星 1/2 的横长(或纵长)减一(如题目中的图).给出一个 n*m 的图,判断是不是每一个 '*' 都能属于 ...
- codeforces 1015E1&&E2
E1. Stars Drawing (Easy Edition) time limit per test 3 seconds memory limit per test 256 megabytes i ...
- Codeforces Round #574 (Div. 2) D1. Submarine in the Rybinsk Sea (easy edition) 【计算贡献】
一.题目 D1. Submarine in the Rybinsk Sea (easy edition) 二.分析 简单版本的话,因为给定的a的长度都是定的,那么我们就无需去考虑其他的,只用计算ai的 ...
- Codeforces - 1195D1 - Submarine in the Rybinsk Sea (easy edition) - 水题
https://codeforc.es/contest/1195/problem/D1 给\(n\)个等长的十进制数串,定义操作\(f(x,y)\)的结果是"从\(y\)的末尾开始一个一个交 ...
- Codeforces 263A. Appleman and Easy Task
A. Appleman and Easy Task time limit per test 1 second memory limit per test 256 megabytes input ...
- codeforces#1163C2. Power Transmission (Hard Edition)(计算几何)
题目链接: https://codeforces.com/contest/1163/problem/C2 题意: 给出$n$个点,任意两点连接一条直线,求相交直线的对数 数据范围: $1 \le n ...
- codeforces Equalizing by Division (easy version)
output standard output The only difference between easy and hard versions is the number of elements ...
- Codeforces 1118F1 Tree Cutting (Easy Version) (简单树形DP)
<题目链接> 题目大意: 给定一棵树,树上的点有0,1,2三中情况,0代表该点无色.现在需要你将这棵树割掉一些边,使得割掉每条边分割成的两部分均最多只含有一种颜色的点,即分割后的两部分不能 ...
- CodeForces 690D1 The Wall (easy) (判断连通块的数量)
题意:给定一个图,问你有几个连通块. 析:不用说了,最简单的DFS. 代码如下: #include <bits/stdc++.h> using namespace std; const i ...
随机推荐
- Hexo之更换背景及透明度
Hexo之更换背景及透明度 引入方式 首先,介绍一下引入方式,外部导入css文件,不影响内部配置. 1.创建css文件 创建一个css文件移动到\themes\butterfly\source\css ...
- iView 的后台管理系统简易模板 iview-admin-simple
iview-admin-simple 是基于 iView 官方模板iView admin整理出来的一套后台集成解决方案.iview-admin-simple删除了iView admin的大部分功能,只 ...
- 强网杯 2019]随便注(堆叠注入,Prepare、execute、deallocate)
然后就是今天学的新东西了,堆叠注入. 1';show databases; # 1';show tables; # 发现两个表1919810931114514.words 依次查询两张表的字段 1'; ...
- STM32 单片机的USART的奇偶校验 误区(坑)
当STM32的串口配置成带有奇偶校验位的情况下,需要软件校验是否发生奇偶校验错误,硬件只是置起奇偶校验错误标志位,并将错误的数据放到DR寄存器中,同时置起RXEN标志位,如果使能中断还是会正常进入中断 ...
- 大数据开发--Hbase协处理器案例
大数据开发--Hbase协处理器案例 1. 需求描述 在社交网站,社交APP上会存储有大量的用户数据以及用户之间的关系数据,比如A用户的好友列表会展示出他所有的好友,现有一张Hbase表,存储就是当前 ...
- 016.NET5_MVC_视图组件扩展定制
视图组件 1. 呈现页面响应的某一部分而不是整个响应 2. 包括在控制器和视图之间发生的关注分类和可测试优势 3.可以具有参数和业务逻辑 4. 通常在页面局部调用 如何自定义视图组件? 1.Razor ...
- React tutorial
https://www.algolia.com Build Unique Search ExperiencesHosted Search API that delivers instant and r ...
- github & personal access token
github & personal access token OAuth https://github.com/xgqfrms/webtrc-in-action/issues/1#issuec ...
- js & bitwise operator
js & bitwise operator bitwise operator https://github.com/Advanced-Frontend/Daily-Interview-Ques ...
- nodejs 在windows10中设置动态(视频)壁纸
github 项目地址 node版本 λ node -v v12.16.2 main.js const ffi = require("@saleae/ffi"); const ch ...
