PTA 统计二叉树叶子结点个数

6-2 统计二叉树叶子结点个数 (10 分)

 

本题要求实现一个函数，可统计二叉树的叶子结点个数。

函数接口定义：

int LeafCount ( BiTree T);

T是二叉树树根指针，函数LeafCount返回二叉树中叶子结点个数，若树为空，则返回0。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;
typedef struct BiTNode
{
	ElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

BiTree Create();/* 细节在此不表 */

int LeafCount ( BiTree T);

int main()
{
	BiTree T = Create();

	printf("%d\n", LeafCount(T));
	return 0;
}
/* 你的代码将被嵌在这里 */

输出样例（对于图中给出的树）：

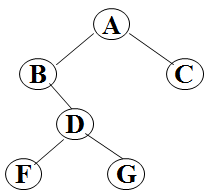
3

int LeafCount ( BiTree T){
    if(T==NULL)
        return 0;
    if(T->lchild==NULL&&T->rchild==NULL){
        return 1;
    }
    else
        return LeafCount(T->lchild)+LeafCount(T->rchild);
}