4.28 省选模拟赛 负环 倍增 矩阵乘法 dp

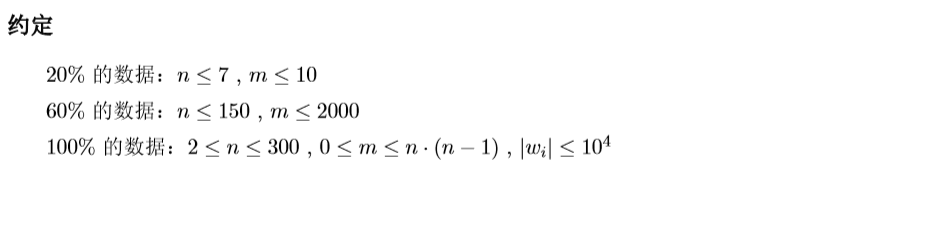
容易想到 这个环一定是简单环。

考虑如果是复杂环 那么显然对于其中的第一个简单环来说 要么其权值为负 如果为正没必要走一圈 走一部分即可。

对于前者 显然可以找到更小的 对于第二部分是递归定义的。

综上 这个环是一个简单环。

那么最多有n个点。

考虑枚举起点 然后 设f[i][j][k]表示从i到j经过k条边的最短路。

容易发现最终的答案为 f[i][i][w]<0 w.

不过这样做是n^4的。

考虑优化 容易想到二分 而上述状态其实本质上是一个矩阵乘法。

那么我们可以矩阵乘法在n^3logn的时间内得到二分出答案的矩阵。

但是这样正确性有点问题。考虑二分的答案并没有一定的单调性。

一个负环大小可能为3 长度为4时可能没有负环。

更改状态比较好 设f[i][j][k]表示从i到j <=k条边的最短路

这样负环就可以被我们保留下来了 关于这个转移 一个比较大胆的想法是 每次矩阵乘法之后对原矩阵取min.

看起来毫无道理 但是 容易发现这个取min操作相当于 做矩阵乘法时 对角线的值全部为0.

至此我们得到了一个普通意义 即 自己到自己有一个0条边的东西。

如果我们要求的答案为mid 那么显然 mid可以由两个小于mid的最短路组成。

从最优性来看这显然存在。所以这样做是正确的。

不过还需要优化复杂度。

考虑倍增出答案。预处理出矩阵即可。

复杂度n^3log.

const int MAXN=310,G=3;
int n,m,maxx,ans;
int b[MAXN][MAXN],c[MAXN][MAXN];
int a[12][MAXN][MAXN];
int main()
{
	freopen("cycle.in","r",stdin);
	freopen("cycle.out","w",stdout);
	memset(a,0x3f,sizeof(a));
	memset(b,0x3f,sizeof(b));
	get(n);get(m);
		rep(1,n,i)rep(1,n,j)a[0][i][j]=INF;
	rep(1,m,i)
	{
		int get(x),get(y),get(z);
		a[0][x][y]=min(a[0][x][y],z);
	}
	rep(1,n,i)a[0][i][i]=0,b[i][i]=0;
	maxx=9;
	rep(1,maxx,w)
	{
		rep(1,n,i)rep(1,n,j)
		{
			int ww=INF;
			rep(1,n,k)ww=min(ww,a[w-1][i][k]+a[w-1][k][j]);
			a[w][i][j]=ww;
		}
	}
	int flag=0;
	rep(1,n,i)if(a[maxx][i][i]<0)flag=1;
	if(!flag){puts("0");return 0;}
	fep(maxx,0,w)
	{
		rep(1,n,i)rep(1,n,j)
		{
			int ww=INF;
			rep(1,n,k)ww=min(ww,b[i][k]+a[w][k][j])%mod;
			c[i][j]=ww;
		}
		flag=0;
		rep(1,n,i)if(c[i][i]<0){flag=1;break;}
		if(flag)continue;
		rep(1,n,i)rep(1,n,j)b[i][j]=c[i][j];
		ans=ans|(1<<w);
	}
	put(ans+1);
	return 0;
}