【洛谷】 3264 [JLOI2015] 管道连接

前言：

 

 

如果还不知道斯坦纳树的童鞋可以看这两篇博客：

我的：https://blog.csdn.net/jerry_wang119/article/details/80001711

我一开始学习的：https://blog.csdn.net/wu_tongtong/article/details/78992913

这道题，在我学习斯坦纳树之前就翻到了，是在洛谷上搜状压的时候看到的。那个时候还不知道斯坦纳树是个什么玩意，不过马上进行了学习。

然而学习了之后也没有什么卵用，发现并不只是斯坦纳树这么简单呐！

 

 

题解：

 

 

由于存在相同频率之间的连通，所以和一般的斯坦纳树是不同的（发现斯坦纳树所指定的结点频率是相同的），需要二次DP。

 

首先跑一遍斯坦纳树的板子，这就求出了 以某一个结点为树根并加入一些边使某几个点连通的最小值，那么我们可以用这个去更新另一个 DP 数组：Ans（S）。

方程：Ans（S）= minx（Ans（S），dp（i，S））；

定义 DP 数组 Ans （S），表示使状态 S 中所有点连通的最小费用，注意，这个 DP 的过程是有条件的：

 

首先枚举 S 集合（指定点集合），这个将这个状态 S 进行更新的条件是 S 必须：对于一个频率，要么包含该频率中的所有指定点，要么不包含于这个频率的任意结点！

 

接着枚举 S 的子集，这个子集 S1 也是要有条件的，也是 必须：对于一个频率，要么包含该频率中的所有指定点，要么不包含于这个频率的任意结点！

 

得到DP方程：Ans（S） = min（Ans（S），Ans（S1）+Ans（S^S1））；

 

这样最后的答案就是 Ans（1<<（p）-1）；

 

为什么要这样做呢？这样做不是和斯坦纳树中的 dp（i，S）数组重复了吗？

 

然而却有很大的区别，这样的 Ans（S）是使得 S 中相同的频率连通，而不是 S 中的所有点都连通！因为用于更新 S 的子集也满足这个条件，而 子集 和 子集对于 S 的补集没有联系，换句话说，两个子集内结点的连通互补干涉。

 

而加上频率的限制：

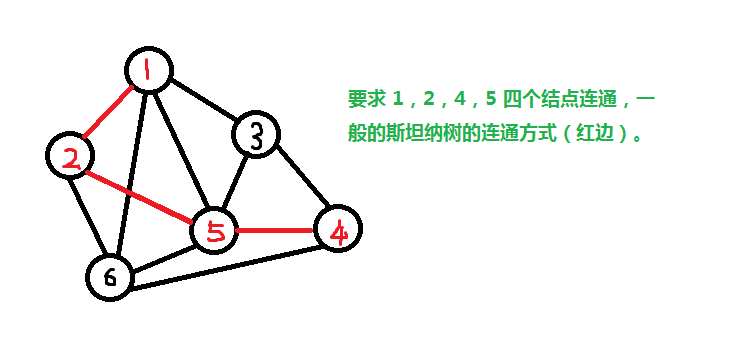
可以看出我们完全不用连边 2-5，因为这条边不改变相同频率的连通性！

所以带条件 Ans（S）经过DP更新后一定是最优解，并且保证没有额外边。

代码：

#include <bits/stdc++.h>

std :: queue < int >  q ;

const  int  N =  +  ;

struct  node {
    int  id , clr ;
}
dot [  ] ;

int  head [ N <<  ] , nxt [ N <<  ] , dis [ N <<  ] , to [ N <<  ] , cn ;
int  dp [ N ] [  <<  ] , ans [  <<  ] , cnt [  ] , sum [  ] , n , m , p , S , x , y , w , inf ;
bool  vis [ N ] , ck [  <<  ] ;

int  minx ( int  a , int  b ) {
    return  a > b ? b : a ;
}

void  create ( int  u , int  v , int  d ) {
    cn ++ ;
    to [ cn ] = v ;
    dis [ cn ] = d ;
    nxt [ cn ] = head [ u ] ;
    head [ u ] = cn ;
}

void  spfa ( int  S ) {
    for ( int  i =  ; i <= n ; i ++ )
        if ( dp [ i ] [ S ] < inf )
            vis [ i ] = true , q . push ( i ) ;
    while ( ! q . empty ( ) ) {
        int  v , tmp = q . front ( ) ;
        q . pop ( ) ; vis [ tmp ] = false ;
        for ( int  i = head [ tmp ] ; i ; i = nxt [ i ] ) {
            v = to [ i ] ;
            if ( dp [ v ] [ S ] > dp [ tmp ] [ S ] + dis [ i ] ) {
                dp [ v ] [ S ] = dp [ tmp ] [ S ] + dis [ i ] ;
                if ( ! vis [ v ] ) {
                    vis [ v ] = true ;
                    q . push ( v ) ;
                }
            }
        }
      }
}

bool  check ( int  S ) {
    memset ( cnt ,  , sizeof ( cnt ) ) ;
    for ( int  i =  ; i <= p ; i ++ )
        if ( S & (  << ( i -  ) ) )
            cnt [ dot [ i ] . clr ] ++ ;
    for ( int  i =  ; i <=  ; i ++ )
        if ( cnt [ i ]  &&  cnt [ i ]  !=  sum [ i ] )
            return   ;
    return   ;
}

int  main ( ) {

    scanf ( "%d%d%d" , & n , & m , & p ) ;
    memset ( dp ,  /  , sizeof ( dp ) ) ;
    inf = dp [  ] [  ] ;
    S = (  << p ) -  ;
    for ( int  i =  ; i <= m ; i ++ ) {
        scanf ( "%d%d%d" , & x , & y , & w ) ;
        create ( x , y , w ) ;
        create ( y , x , w ) ;
    }
    for ( int  i =  ; i <= p ; i ++ ) {
        scanf ( "%d%d" , & dot [ i ] . clr , & dot [ i ] . id ) ;
        sum [ dot [ i ] . clr ] ++ ;
    }
    for ( int  i =  ; i <= p ; i ++ )
        dp [ dot [ i ] . id ] [  << ( i -  ) ] =  ;
    for ( int  s =  ; s <= S ; s ++ ) {
        for ( int  i =  ; i <= n ; i ++ )
            for ( int  s1 = s ; s1 ; s1 = ( s1 -  ) & s )
                dp [ i ] [ s ] = minx ( dp [ i ] [ s ] , dp [ i ] [ s1 ] + dp [ i ] [ s ^ s1 ] ) ;
        spfa ( s ) ;
    }
    memset ( ans ,  /  , sizeof ( ans ) ) ;
    for ( int  s =  ; s <= S ; s ++ )
        for ( int  i =  ; i <= n ; i ++ )
            ans [ s ] = minx ( ans [ s ] , dp [ i ] [ s ] ) ;
    for ( int  s1 =  ; s1 <= S ; s1 ++ )
        if ( check ( s1 ) )
            ck [ s1 ] = true ;
    for ( int  s =  ; s <= S ; s ++ )
        if ( ck [ s ] )
            for ( int  s1 = s ; s1 ; s1 = ( s1 -  ) & s )
                if ( ck [ s1 ] )
                    ans [ s ] = minx ( ans [ s ] , ans [ s1 ] + ans [ s ^ s1 ] ) ;
    printf ( "%d" , ans [ S ] ) ;
    return   ;
}

Ans for this

要开O2，因为STL队列很慢。