bzoj2006: [NOI2010]超级钢琴（堆+RMQ）

　　和上一道题同类型...都是用堆求第k大

　　考虑对于每一个r，怎么求出一个最优的l。显然只需要求出前缀和，用RMQ查询前面最小的l的前缀和就好了。但是对于一个r，每个l只能选一次，选了一次之后，考虑怎么把l删掉。假设一个r，能选的l的区间在[A,B]，那么选了l之后，这个区间就变成了[A,l-1]∪[l+1,B]，所以我们可以构造一个四元组(sum, l, r, x)表示对于一个右端点x，能选择的左端点在[l,r]，且最大的值为sum。用堆找出sum最大的二元组之后，求出这个sum的左端点y，然后把这个四元组拆成两个，能选择区间分别为[l,y-1]和[y+1,r]，然后求出sum再加进堆里，取k次即得答案。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<queue>
#include<cmath>
#define ll long long
using namespace std;
const int maxn=;
struct poi{int sum, l, r, x;};
priority_queue<poi>q;
int n, k, l, r;
int sum[maxn], f[maxn][];
ll ans;
void read(int &k)
{
    int f=; k=; char c=getchar();
    while(c<'' || c>'') c=='-' && (f=-), c=getchar();
    while(c<='' && c>='') k=k*+c-'', c=getchar();
    k*=f;
}
inline int min(int a, int b){return sum[a]<sum[b]?a:b;}
inline int querymin(int l, int r)
{
    bool flag=; if(!l) l++, flag=;
    if(l>r) return ;
    int k=log2(r-l+), ans=min(f[l][k], f[r-(<<k)+][k]);
    return flag?min(, ans):ans;
}
bool operator<(poi a, poi b) {return a.sum<b.sum;}
int main()
{
    read(n); read(k); read(l); read(r);
    for(int i=;i<=n;i++) read(sum[i]), sum[i]+=sum[i-], f[i][]=i;
    for(int j=;j<=log2(n);j++)
    for(int i=;i<=n-(<<j)+;i++)
    f[i][j]=min(f[i][j-], f[i+(<<(j-))][j-]);
    for(int i=l;i<=n;i++) q.push((poi){sum[f[i][]]-sum[querymin(max(, i-r), i-l)], max(, i-r), i-l, i});
    for(int i=;i<=k;i++)
    {
        poi t=q.top(); q.pop();
        ans+=t.sum; int x=querymin(t.l, t.r);
        if(x!=t.l) q.push((poi){sum[f[t.x][]]-sum[querymin(t.l, x-)], t.l, x-, t.x});
        if(x!=t.r) q.push((poi){sum[f[t.x][]]-sum[querymin(x+, t.r)], x+, t.r, t.x});
    }
    printf("%lld\n", ans);
    return ;
}

　　为什么要求sum？这个不是可以O(1)算的吗？

　　一开始我写的就是用子程序算sum，把四元组变成三元组，要求sum的时候再临时调用子程序计算，导致的结果就是TLE！

　　虽然写了RMQ查询是O(1)的，但是多次调用子程序严重拖慢程序速度！宁愿多一维先计算出sum，这样调用子程序的次数会少很多，常数也就会小很多...

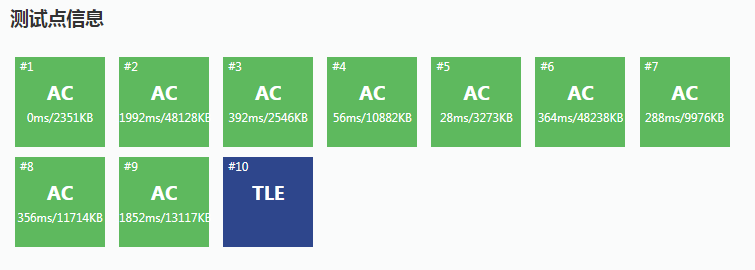
　　上方是先计算了sum的，下方是临时调用子程序计算sum的，可以发现常数大了一倍还多...而且我已经不是第一次因为多次调用子程序被卡常了T T