标签页QTabWidget

样式：

 import sys
 from PyQt5.QtGui import QIcon
 from PyQt5.QtWidgets import QApplication, QWidget, QTabWidget, QLabel, QLineEdit, QDateEdit, \
     QComboBox, QTextEdit, QGridLayout

 class Demo(QTabWidget):#继承标签页类
     def __init__(self):
         super(Demo, self).__init__()
         self.resize(400,200)  #设置标签页面的大小
         self.tab1 = QWidget()  #实例化一个窗口，做为标签1的窗口

         self.tab2 = QWidget()
         self.tab3 = QTextEdit()

         self.tab1_init()
         self.tab2_init()
         #
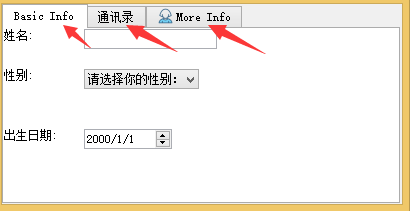
         self.addTab(self.tab1, 'Basic Info')  #添加标签
         #添加之后才会显示
         #参数1：是QWidget窗口或控件
         #参数2：标签显示的文本

         self.addTab(self.tab2, '通讯录')
         self.addTab(self.tab3, QIcon('f1.ico'), 'More Info')  #添加标签
         #QIcon('f1.ico')   标签图标

         self.currentChanged.connect(lambda: print(self.currentIndex()))  # 用户点击不同标签页时，都会触发信号
         #self.currentIndex()  返回标签项序列号

     def tab1_init(self):
         name_label = QLabel('姓名:', self.tab1)
         gender_label = QLabel('性别:', self.tab1)
         gender_label.move(0,40)

         bd_label = QLabel('出生日期:', self.tab1)
         bd_label.move(0,100)
     # #
         name_line = QLineEdit(self.tab1)
         name_line.move(80,0)
     #
         items = ['请选择你的性别：', 'Female', 'Male']
         gender_combo = QComboBox(self.tab1)
         gender_combo.addItems(items)
         gender_combo.move(80,40)

         bd_dateedit = QDateEdit(self.tab1)
         bd_dateedit.move(80,100)

     def tab2_init(self):
         tel_label = QLabel('电话:', self.tab2)
         mobile_label = QLabel('手机:', self.tab2)
         mobile_label.move(0,40)

         add_label = QLabel('地址:', self.tab2)
         add_label.move(0,80)

         tel_line = QLineEdit(self.tab2)
         tel_line.move(60,0)
         mobile_line = QLineEdit(self.tab2)
         mobile_line.move(60,40)
         add_line = QLineEdit(self.tab2)
         add_line.move(60,80)

 if __name__ == '__main__':
     app = QApplication(sys.argv)
     demo = Demo()
     demo.show()
     sys.exit(app.exec_())