HDU 5093 Battle ships(二分图最大匹配)

题意：一个m行n列的图由#、*、o三种符号组成，分别代表冰山、海域、浮冰，问最多可放的炮舰数（要求满足以下条件）

1、炮舰只可放在海域处

2、两个炮舰不能放在同一行或同一列(除非中间隔着一个或多个冰山)

分析：

1、如果单纯只考虑不能放在同一行同一列，那就是行号与列号的匹配，原理与UVALive 6811 Irrigation Line(二分图最小点覆盖--匈牙利算法)相同。

2、但现在隔着冰山可以放置炮舰，那假设某一行被冰山分隔成两部分，这一行的前半部分和后半部分可以看做是两行，再应用“行号”与“列号”的匹配的原理

3、既然要行号与列号匹配，那就要分别按照行和列给图标号

举例如下：

(1)若按行，则将海域从1开始标号，如果是连续的海域那标号相同，若有冰山分隔，标号加1.

PS:例如第三行22#3，此处2是形式意义上的第二行，因为有上述放置炮舰的原则，可以理解为是可以放置炮舰的第2行，而由于有冰山分隔，所以这一行的前后互不干扰，因此3可以理解为是可以放置炮舰的第3行

(2)按列同理

4、理论上讲海域可以放置炮舰，也就是说，有标号的地方可以放置炮舰，每一个放置的地方都是一个行号与列号的匹配，由此可得如下匹配

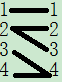
5、一条连线代表一个可放置的炮舰，求最大匹配即可

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define Min(a, b) a < b ? a : b
#define Max(a, b) a < b ? b : a
typedef long long ll;
typedef unsigned long long llu;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const ll LL_INF = 0x3f3f3f3f3f3f3f3f;
const ll LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {, , -, };
const int dc[] = {-, , , };
const double pi = acos(-1.0);
const double eps = 1e-;
const int MAXN =  + ;
const int MAXT =  + ;
using namespace std;
char a[MAXN][MAXN];
int x[MAXN][MAXN];
int y[MAXN][MAXN];
int mp[MAXT][MAXT];
bool used[MAXT];
int match[MAXT];
int m, n, cnt1, cnt2;
void deal_row(){
    cnt1 = ;
    for(int i = ; i < m; ++i){
        bool flag = false;
        for(int j = ; j < n; ++j){
            if(a[i][j] == '*'){
                x[i][j] = cnt1;
                flag = true;
            }
            if(a[i][j] == '#'){
                ++cnt1;
                flag = false;
            }
        }
        if(flag) ++cnt1;
    }
}
void deal_column(){
    cnt2 = ;
    for(int i = ; i < n; ++i){
        bool flag = false;
        for(int j = ; j < m; ++j){
            if(a[j][i] == '*'){
                y[j][i] = cnt2;
                flag = true;
            }
            if(a[j][i] == '#'){
                ++cnt2;
                flag = false;
            }
        }
        if(flag) ++cnt2;
    }
}
bool Find(int x){
    for(int i = ; i < cnt2; ++i){
        if(mp[x][i] && !used[i]){
            used[i] = true;
            if(!match[i] || Find(match[i])){
                match[i] = x;
                return true;
            }
        }
    }
    return false;
}
void solve(){
    int cnt = ;
    for(int i = ; i < cnt1; ++i){
        memset(used, false, sizeof used);
        if(Find(i)) ++cnt;
    }
    printf("%d\n", cnt);
}
int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        memset(a, , sizeof a);
        memset(x, , sizeof x);
        memset(y, , sizeof y);
        memset(mp, , sizeof mp);
        memset(match, , sizeof match);
        scanf("%d%d", &m, &n);
        for(int i = ; i < m; ++i)
            scanf("%s", a[i]);
        deal_row();
        deal_column();
        for(int i = ; i < m; ++i){
            for(int j = ; j < n; ++j){
                if(a[i][j] == '*'){
                    mp[x[i][j]][y[i][j]] = ;
                }
            }
        }
        solve();
    }
    return ;
}