HDU 4662 MU Puzzle 2013 Multi-University Training Contest 6

现在有一个字符串”MI”，这个字符串可以遵循以下规则进行转换：

1、Mx 可以转换成 Mxx ，即 M 之后的所有字符全部复制一遍（MUI –> MUIUI）

2、III 可以转换成 U。

3、UU 可以直接消除

现在你的任务是，给定你另外一串字符串，请判断能否从“MI”按照如上规则用有限的步骤转化得出。

（先吐个槽，出题人是MIUI的粉丝还是肿么？？）

进入正题，从数据大小为 10⁶ 来看就知道这个肯定有公式。下面来讲一下肿么推出来的。

首先，三个 I 可以转化出一个 U 。所以先对给出的目标字符串进行转换，统计出 I 的个数，而 U 的话记为三个 Ｉ就好了（为什么这样呢？因为 U 只能通过 III 来进行转换，所以目标串中是的 U 可以直接逆转化为三个 I ，至于为什么这里要统计 I 的个数在下面几步我会说）。

接下来看第一条转化规则，所有 M 之后的字符复制一份。通过模拟可以知道，这样就限制死 I 的个数（在没有转化为 U 的情况下）为 2^m （m ∈ [0, +∞]）。

然后，注意第三条，因为两个 U 可以直接消除，结合第二条可以知道，六个 I 可以直接消除，因此这条会导致第一步中统计出的个数不是上一步中说的那样，是 2^m 。

通过上面三步，我们可以得到如下的公式：

得到此公式之后，两边同时除以 2 ，得到公式：

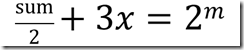
（为什么是 m 不是 m – 1 ？这里 m 和 x 都是未知数，所以 m 和 m – 1 在这里是一样的）

接下来的步骤我直接用公式表示了，只是一个推导过程：

记 Q = sum / 2       R = 2^m

式子转化为 Q + 3x = R

因为 3 是无法被 R 整除的，所以必定会有 （q + 3）* x = R (其中 q = Q / x)，而 x 一定是 2 的整次方数。

所以可以把式子化成这样： q + 3 = R (为什么还是R，理由之前说过了)

到了这一步，做法就已经很明了了：把第一步得到的 sum 一直除以二，直到不能除为止。然后 sum += 3，判断是否为 R 就OK。

这一步可能又有问题，为什么不在一开始得到 sum + 6x = R 的时候就这么做，对此，我只能说Orz，数据爆了。

最后一个需要注意的地方是，要对目标串有多个 M 的情况进行判定。

附AC代码（偷个懒，贴上队友的）

   1: #include <stdio.h>

   2: #include <string.h>

   3: #include <math.h>

   4: #include <stdlib.h>

   5: #include <algorithm>

   6: #include <iostream>

   7: #include <string>

   8: #include <list>

   9: #include <vector>

  10: #include <queue>

  11: #include <map>

  12: #include <set>

  13:  

  14: using namespace std;

  15:  

  16: //#define DEBUG

  17:  

  18: bool judge(int n)

  19: {

  20:     if (n == 1)

  21:         return true;

  22:     if (!n || n % 2)

  23:         return false;

  24:     while (n % 2 == 0)

  25:         n /= 2;

  26:     n += 3;

  27:     int one = 1;

  28:     for (int i = 0; i < 32; i++)

  29:         if ((((one << i) - n) % 6 == 0) && ((one << i) >= n))

  30:             return true;

  31:     return false;

  32: }

  33:  

  34: int main()

  35: {

  36: #ifdef DEBUG

  37:     freopen("cin.txt", "r", stdin);

  38:     freopen("cout.txt", "w", stdout);

  39: #endif

  40:     int T;

  41:     for (scanf("%d", &T); T--;)

  42:     {

  43:         int sum = 0;

  44:         string line;

  45:         cin >> line;

  46:         if (line[0] != 'M')

  47:             puts("No");

  48:         else

  49:         {

  50:             bool flag = true;;

  51:             for (int i = 1; i < line.size(); i++)

  52:             {

  53:                 if (line[i] == 'M')

  54:                     flag = false;

  55:                 sum += (line[i] == 'I' ? 1 : 3);

  56:             }

  57:             puts(flag && judge(sum) ? "Yes" : "No");

  58:         }

  59:     }

  60:     return 0;

  61: }