[bzoj 3226]校门外的区间
题意
输出最后的集合
题解
校门外的树会做吧
区间知道是什么东西吧
校门外的区间会做了吧

昨天做个大线段树没做出来,今天做个小线段树压压惊
py一下输入数据,然后操作变成:
U 区间涂1
I 两侧区间涂0
D 区间涂0
C 两侧涂0,中间取反
S 区间取反
#include<map>
#include<stack>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<complex>
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;
#define inf 1001001001
#define infll 1001001001001001001LL
#define ll long long
#define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl
#define gmax(a,b) (a)=max((a),(b))
#define gmin(a,b) (a)=min((a),(b))
#define Ri register int
#define gc getchar()
#define il inline
il int read(){
Ri x=0,f=0;char ch;
while(!isdigit(ch=gc))if(ch=='(')f=-1;
while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}
if(ch==')')f=1;
return x*2-f;
}
#define gi read()
#define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
#define N 131073
char ch[5];
struct seg{int l,r,val,tag,rev;}t[4*N];
void build(int k,int l,int r){
t[k]=(seg){l,r,0,-1,0};
if(l==r) return;
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
}
void pushdown(int k){
int tag=t[k].tag,rev=t[k].rev;
t[k].tag=-1;t[k].rev=0;
if(t[k].l==t[k].r){
if(tag!=-1)t[k].val=tag;
t[k].val^=rev;;
return;
}
if(tag!=-1){
t[k<<1].tag=t[k<<1|1].tag=tag;
t[k<<1].rev=t[k<<1|1].rev=0;
}
t[k<<1].rev^=rev;t[k<<1|1].rev^=rev;
}
int query(int k,int x){
pushdown(k);
int l=t[k].l,r=t[k].r;
if(l==r) return t[k].val;
int mid=(l+r)>>1;
if(x<=mid)
return query(k<<1,x);
else
return query(k<<1|1,x);
}
void modify(int k,int x,int y,int val){
if(y<x)return;
pushdown(k);
int l=t[k].l,r=t[k].r;
if(l==x&&y==r){
if(val==-1) t[k].rev^=1;
else t[k].tag=val;
return;
}
int mid=(l+r)>>1;
if(y<=mid)
modify(k<<1,x,y,val);
else if(x>mid)
modify(k<<1|1,x,y,val);
else {
modify(k<<1,x,mid,val);
modify(k<<1|1,mid+1,y,val);
}
}
int main(){
build(1,1,N);
while(scanf("%s",ch)!=EOF){
int a=gi,b=gi;
a+=2;b+=2;
switch(ch[0]){
case 'U':modify(1,a,b,1);break;
case 'I':modify(1,1,a-1,0);modify(1,b+1,N,0);break;
case 'D':modify(1,a,b,0);break;
case 'C':modify(1,1,a-1,0);modify(1,b+1,N,0);modify(1,a,b,-1);break;
case 'S':modify(1,a,b,-1);break;
}
}
int start=-1,last=-1,flag=0;
for(int i=1;i<=N;i++)
if(query(1,i)){
if(start==-1)start=i;
last=i;
}
else{
if(start!=-1){
if(flag)printf(" ");else flag=1;
if(start&1) printf("(");
else printf("[");
printf("%d,%d",start/2-1,(last+1)/2-1);
if(last&1)printf(")");
else printf("]");
}
last=start=-1;
}
if(!flag)puts("empty set");
return 0;
}
[bzoj 3226]校门外的区间的更多相关文章
- bzoj 3226 [Sdoi2008]校门外的区间(线段树)
3226: [Sdoi2008]校门外的区间 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 615 Solved: 227[Submit][Stat ...
- 3226. [SDOI2008]校门外的区间【线段树】
Description 受校门外的树这道经典问题的启发,A君根据基本的离散数学的知识,抽象出5种运算维护集合S(S初始为空)并最终输出S.现在,请你完成这道校门外的树之难度增强版——校门外的区间. ...
- BZOJ-3226 校门外的区间 线段数+拆点(类似的思想)
shabi题....bzoj关键字检查freopen??可怕,,1A的卡了一小时.... 3226: [Sdoi2008]校门外的区间 Time Limit: 10 Sec Memory Limit: ...
- BZOJ 3226: [Sdoi2008]校门外的区间
题目链接:http://www.lydsy.com:808/JudgeOnline/problem.php?id=3226 题意:初始集合S为空.模拟四种集合操作:集合并.交.差.补集并. 思路:区间 ...
- 3226: [Sdoi2008]校门外的区间
链接 思路 bug漫天飞... 维护一颗线段树,支持区间赋值,和区间异或.因为会处理到一些方括号还是圆括号的问题,所以对于每一个下标都乘2,假设中间有一个.5即可,都变成了方括号,输出在处理一下. U ...
- BZOJ3226[Sdoi2008]校门外的区间 题解
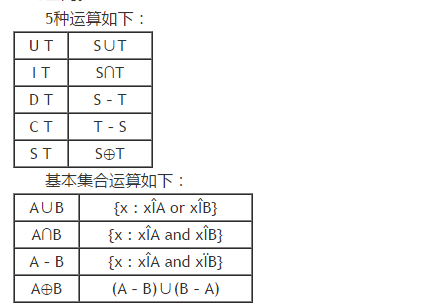
题目大意: 有5种运算维护集合S(S初始为空)并最终输出S. 5种运算如下: U T S∪T I T S∩T D T S-T C T T-S S T S⊕T 基本集合运算如下: A∪B {x : ...
- 「BZOJ3226」[Sdoi2008]校门外的区间
题目 首先是开闭区间的处理,我们把\(1.5\)这种数加进来,用\([1.5,6]\)来表示\((2,6]\) 根据离散数学的基本知识,尝试把五个操作转化成人话 把\([x,y]\)变成\(1\) 把 ...
- [SDOI2008] 校门外的区间 - 线段树
U T 即将区间 \(T\) 范围赋值为 \(1\) I T 即将区间 \(U - T\) 范围赋值为 \(0\) D T 即将区间 \(T\) 赋值为 \(0\) C T 由于 \(S=T-S=T( ...
- BZOJ3226: [Sdoi2008]校门外的区间
感觉很有趣的题呢. 每个点拆成两个,线段树维护. 不过这题难点其实在输入输出. #include<bits/stdc++.h> #define N (1<<17) #defin ...
随机推荐
- jQuery 遍历each()的使用方法
.each()是一个for循环的包装迭代器.each()通过回调的方式处理,并且会有2个固定的实参,索引与元素(从0开始计数).each()回调方法中的this指向当前迭代的dom元素 遍历方法: & ...
- 常用按键ASCII码
ESC 27回车 13TAB 9Caps Lock 20Shift $10 Ctrl 17Alt 18空格 VK_SPACE 32退格 VK_BACK 8左徽标 VK_LWIN 91右徽标 VK_RW ...
- C# 平时碰见的问题【2】
问题1 修改命名空间后 .ashx 类型创建失败 [情景] 在调整前后台项目结构的时候,修改了默认命名空间(XXX.Admin 修改成XXX.Web),结果调试的时候发现XXX.Admin.Ajax. ...
- mysql数据库开发规范
对规范的遵守可用二八原则,不要教条.为满足实际需求 可忽视部分规范. 1.索引规范 *目标 |--利用最小的索引成本找到需要的行记录 *原则 |--做前缀匹配 |--选择区分度高的列做前缀索引列 |- ...
- 在Unity项目中使用Git
(搬运自我在SegmentFault的博客) 本文参考了Unity官网的Mastering Unity Project Folder Structure - Version Control Syste ...
- jquery的异步获取返回值为中文时乱码解决方法
用jqgrid异步获取列表值,遇到个问题,服务器端从数据库取到的数据没有出现中文乱码问题(日志打出来是没有乱码的),但是异步传到客户的时候却出现了乱码. 服务器端已经编码过了(UTF-8编码).开始一 ...
- chkconfig 命令详解
chkconfig命令主要用来更新(启动或停止)和查询系统服务的运行级信息.谨记chkconfig不是立即自动禁止或激活一个服务,它只是简单的改变了符号连接. 使用语法: chkconfig [--a ...
- golang实现ping命令
// Copyright 2009 The Go Authors. All rights reserved.// Use of this source code is governed by a B ...
- Mac下如何显示隐藏文件/文件夹_百度经验
在应用程序里打开终端, cd 你的文件夹名 ls -a 即可显示该文件夹下的所有隐藏文件 如果你想打开整个系统的隐藏文件可以在终端下输入以下命令: defaults write com.apple ...
- MS Chart-按照数据库的最大最小时间设置X轴label.
核心代码: Chart1.ChartAreas[0].AxisX.Interval = (Front_Max - Front_Min).Days / 2; Chart1.ChartAreas[0].A ...
