Wannafly挑战赛25 B.面积并

链接

[https://www.nowcoder.com/acm/contest/197/B]

分析

特殊优先考虑

首先考虑r>=l这种情况就是圆的面积了

第二就是r<=内切圆的半径，这个直接是n多边形的面积了

第三种就是介于上面二者之间了

关键就是怎么求弓形的面积，也就是扇形面积减去三角形面积了



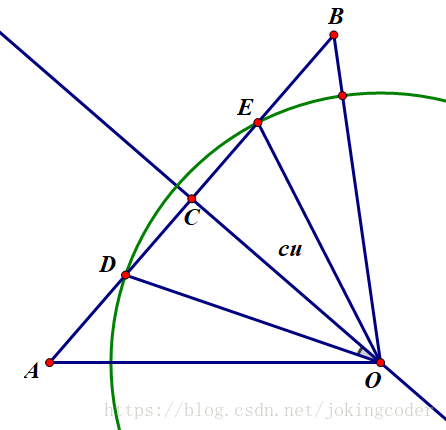
先求出CO和CD

后面就好办了

注意这里的扇形公式S扇=(夹角/360)πR² 化简 π和360约分得到二分之一，二分之一夹角正是<DOC,这里是关键

看代码吧

对特别注意精度用long double

#include<bits/stdc++.h>
using namespace std;
#define pi acos(-1.0)
int main() {

    long double n, l, r;
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> n >> l >> r;

    long double h = l*cos(pi/n);//CO 也就是内切圆半径
    long double d = sqrt(l*l - h*h);//勾股定理求CD，底的一半
    long double ans = 0.5*sin(2*pi/n)*l*l;//把正多边形分角成n个三角形的面积
    if(r >=l) ans = pi*r*r;//第一种
    else if (r<=h) ans*=n;//第二种
    else {
        long double DOC=acos(h/r); //这里很关键，计算角DOC
		//这时候扇形面积就可以根据公式化简了
        long double dd=sqrt(r*r - h*h);
        ans+=DOC*r*r - dd*h;//扇形-三角形，因为dd是底的一半不用除二
        ans*=n;
    }

    cout << fixed << setprecision(2) << ans << endl;
    return 0;
}