解答：

评：这里涉及到e有关的极限的单调性，求导数得：

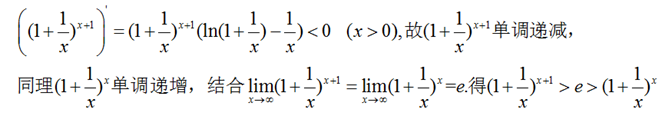
MT【8】和e有关的一个极限的更多相关文章

  1. 0.9循环=lim(n趋于无穷大)(1-1/10的n次方)，所以这是一个极限问题

    0.9循环=lim(n趋于无穷大)(1-1/10的n次方),所以这是一个极限问题 因为lim(...)(1-1/10的n次方)=1 这意味着维尔斯特拉斯发明极限定义之前,这个等号是不成立的,因为没有极 ...

  2. MT【159】单调有界有极限

    已知数列$\{a_n\}$满足:$a_n>0,a_{n+1}+\dfrac{1}{a_n}<2,n\in N^*$.求证:(1)$a_{n+2}<a_{n+1}<2 (n\in ...

  3. MT【6】等比数列和的极限

    评:利用等比数列求和公式给出所求数列,再利用反证法证明唯一性.这种反证方法印象中本科高等代数里讲初等对称多项式时出现过.

  4. MT【113】无中生有加一个减一个

    代数上可以这么解答:不妨设$x\le y$ 1)若$y-x\le\frac{1}{2},则|f(x)-f(y)|<\frac{1}{2}|x-y|\le\frac{1}{4}$ 2)若$y-x& ...

  5. 禁止MT在公式后面自动添加一个空格

    开始 > 运行,或者win+R,然后输入 regedit,打开注册表编辑器.展开到HKEY_CURRENT_USER\Software\Design Science\DSMT6\WordComm ...

  6. OO，OO以后，及其极限

    1.什么是软件开发? 软件开发的过程就是人们使用各种计算机语言将人们关心的现实世界映射到计算机世界的过程: 现在的计算机的数学理论基础是由计算机的开山鼻祖,大名鼎鼎的图灵于1937年提出的图灵机模型. ...

  7. 数学——函数极限知识以及sympy库的limit

    函数极限与Sympy库 欢迎访问我的博客 这部分可以参考sympy库中的limit 在$z_0$点处计算$e(z)$函数的极限 \(\lim_{z \to z_0} e(z)\) = limit(e, ...

  8. 【深度学习与神经网络】深度学习的下一个热点——GANs将改变世界

    本文作者 Nikolai Yakovenko 毕业于哥伦比亚大学,目前是 Google 的工程师,致力于构建人工智能系统,专注于语言处理.文本分类.解析与生成. 生成式对抗网络-简称GANs-将成为深 ...

  9. linux-web基础

    web基础 [TOC] 网上冲浪 网上冲浪:在Internet互联网上获取各种信息,进行工作.娱乐,在英文中上网是" surfing the internet",因"su ...

随机推荐

  1. 『转』MySQL存储过程语法例子

    原文地址:http://blog.chinaunix.net/uid-540802-id-138873.html ------------------------- 自动生成随机数据存储过程 ---- ...

  2. java算法----排序----（4）快速排序

    package log; public class Test4 { /** * java算法---快速排序 * * @param args */ public static void main(Str ...

  3. SSIS ->> Excel Destination无法接受大于255个字符长度的字符字段（转载）

    从下文的链接中找到一些背景,因为Excel会以前8行作为参考,如果某个字段前8行的最长长度没有超过255个字符,就会报错.如果知道某个字段属于描述性字段,而且字段的数据长度很可能超过255个字符长度, ...

  4. .NET Standard库引用导致的FileNotFoundException探究

    微软近几年推出.NET Standard,将.NET Framework,.NET Core,Xamarin等目标平台的api进行标准化和统一化,极大地方便了类库编写人员的工作.简单的说,类库编写人员 ...

  5. CentOS 7.2:Failed to start IPv4 firewall with iptables

    问题 系统是centos7.2,且已经安装了iptables服务,但是在执行启动命令后,却报了iptables服务无法正常启动的错误. 启动命令如下: systemctl start iptables ...

  6. LVS负载均衡-基础知识梳理

    一. 集群的概念 服务器集群简称集群是一种服务器系统,它通过一组松散集成的服务器软件和/或硬件连接起来高度紧密地协作完成计算工作.在某种意义上,他们可以被看作是一台服务器.集群系统中的单个服务器通常称 ...

  7. scenario testing

    我们的APP“吃了么”是专为爱美食的人打造的,典型的用户自然是那些喜欢美食的“吃货”们,当然也可以为想要快速找到周边餐馆的童鞋提供便利.还有一种典型的用户就是喜欢自己烹调食物的人. 我们整理出来了下面 ...

  8. #个人博客作业Week3——必应词典案例分析

    第一部分 调研以及评测 一.BUG分析   1. 翻译部分原文语言检测部分 1) 症状: 当选择原文语言是简体中文时,输入英文查询,程序不报错,继续翻译,选择其他类型语言也是如此. 且如果出现这种情况 ...

  9. Linux内核分析 笔记七 可执行程序的装载 ——by王玥

    一.预处理.编译.链接和目标文件的格式 (一)可执行程序是怎么得来的? 1. 2.可执行文件的创建——预处理.编译和链接 shiyanlou:~/ $ cd Code                  ...

  10. Proxy 示例

    package cn.proxy03; import java.lang.reflect.InvocationHandler; import java.lang.reflect.Method; imp ...