AtCoder Regular Contest 063 F : Snuke’s Coloring 2 (线段树 + 单调栈)

题意

小 \(\mathrm{C}\) 很喜欢二维染色问题,这天他拿来了一个 \(w × h\) 的二维平面 , 初始时均为白色 . 然后他在上面设置了 \(n\) 个关键点 \((X_i , Y_i)\) , 对于每个关键点他会选择进行下列操作的一个 :

• 将 \(x > X_i\) 的部分染成黑色.
• 将 \(x < X_i\) 的部分染成黑色.
• 将 \(y > Y_i\) 的部分染成黑色.
• 将 \(y < Y_i\) 的部分染成黑色.

现在让你 , 最大化所有操作结束之后白色部分的 周长 如果白色部分没有输出 \(0\)

\((0 \le n ≤ 2 \times 10^5 , 1 \le w,h \le 10^8, 0\le X_i \le w, 0 \le Y_i \le h)\)

题解

我先摘一段 dy0607 的题解qwq (Orz dyy)

题目实际上是要找一个周长最大的矩形 , 内部不包含任何关键点.

可以发现一个小性质 : 答案的下界为 \(2 × (max(w, h) + 1)\) ,

因此这个矩形一定会经过 \(x = \frac{w}{2}\) 或 \(y = \frac{h} {2}\) . 先考虑经过 \(x = \frac{w}{2}\) 的情况 , 另一种情况是一样的.

先将坐标离散化.枚举矩形的上边界 \(y_R\) ,对于每一个下边界 \(y_L\) , 我们可以计算出矩形的最优左边界 \(x_L = min \{X_i |Y_i ∈ [y_L , y_R ], X_i > \frac{w}{2} \}\) , 以 及 右 边 界 \(x_R = max \{X_i |Y_i ∈[y_L , y_R ], X_i ≤ \frac{w} {2} \}\) ,

此时可以找到一个周长为 \(2 × (x R − x L + y R − y L )\) 的矩形.

直接做是 \(O(n^2)\) 的,但该算法可以用线段树优化,在将上边界往上移的过程中动态维护每

个位置的 \(x_L , x_R\) ,并维护全局最小值,不难发现只需要左右各开一个单调栈,在更新单调栈

时在线段树树上进行区间加减即可. \(O(n \log n)\) .

就算没有观察到上面的小性质,也可以多套一层分治解决,复杂度多一个 \(\log\) .

说的很轻松 其实很难理解

\(\Theta(n^2)\) 的算法 就是运用了那个小性质 每次枚举上边界 滑动的时候 一遍更新 一遍算下答案 就行了

我们主要是考虑 \(\Theta(n \log n)\) 的算法 , 如何理解呢 ...

其实我们就是枚举了一个上边界 , 然后对于这个上边界时 所有下边界的最优解都存在线段树中 .

(存的是当前 当前的顶到这里的宽 -下底界的高度 )

---

主要讲一下单调栈是干什么的

其中元素是一个个从栈底到栈顶是逐渐远离中线的线段 .

其中有两个维度 一个是维护这条线段的上端 , 另一个是维护这条线段的这条线段的横坐标 用来算和中线的长度 .

然后维护了这个有什么用呢 0.0 就是你考虑如下一种情况

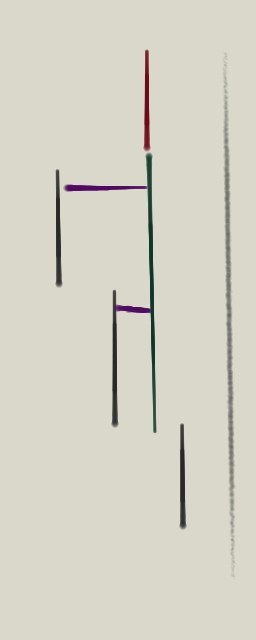
(虚线为中线 黑色 是当前单调栈里的 红色 是现在将过来的一个线段)

---

我们现在要过来的线段 , 将会更新答案 .

所以我们将两个栈顶线段的答案进行更改 , 将这些线段的横着的答案变小它坐标的相应的差值.

这个就可以直接在线段树上做加减法就行了 .

然后我们用这条 绿色 和 红色 的线段一起 共同构成一个新的线段存进单调栈中去 .

---

记得前面线段树存的什么嘛 .

就是一个点当前宽与底坐标的差值 , 然后顶 (就是后一个线段的纵坐标) 又是固定的 那么我们用顶减去底 然后加上当前宽 .

就得到了当前矩形一半周长的最优答案 .

---

然后为了解决两个相邻直接当上下界的答案 , 我们每次结束要在单调栈中多加一个元素 (横坐标为边界) 就行了 .

然后坐标翻转再做一遍 就行了就是可能跨了另一条中线qwq

代码

代码比较巧妙 一定要对着理解!!

#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
using namespace std;

inline bool chkmin(int &a, int b) {return b < a ? a = b, 1 : 0;}
inline bool chkmax(int &a, int b) {return b > a ? a = b, 1 : 0;}

inline int read() {
    int x = 0, fh = 1; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
    for (; isdigit(ch); ch = getchar()) x = (x * 10) + (ch ^ 48);
    return x * fh;
}

void File() {
	freopen ("paint.in", "r", stdin);
	freopen ("paint.out", "w", stdout);
}

const int N = 200010;

int w, h, n;

struct Segment_Tree {
	int maxv[N << 2], add[N << 2];

	void Init() { Set(maxv, 0); Set(add, 0); }

	void Update(int o, int l, int r, int ul, int ur, int uv) {
		if (ul <= l && r <= ur) { maxv[o] += uv; add[o] += uv; return ; }
		int mid = (l + r) >> 1;
		if (ul <= mid) Update(o << 1, l, mid, ul, ur, uv);
		if (ur > mid) Update(o << 1 | 1, mid + 1, r, ul, ur, uv);
		maxv[o] = max(maxv[o << 1], maxv[o << 1 | 1]) + add[o];
	}
} T;

typedef pair<int, int> PII;
#define x first
#define y second
#define mp make_pair
PII lt[N];
PII sta[N], stb[N];
int topa, topb;

int ans = 0;

void Work() {
	sort(lt + 1, lt + 1 + n);

	T.Init();
	topa = topb = 0;

	For (i, 1, n - 1) {
		if (lt[i].y <= h / 2) {
			int Next = i - 1;
			while (topa && lt[i].y > sta[topa].y) {
				T.Update(1, 1, n, sta[topa].x, Next, sta[topa].y - lt[i].y);
				Next = sta[topa].x - 1; -- topa;
			}
			if (Next != i - 1) sta[++ topa] = mp(Next + 1, lt[i].y);
		} else {
			int Next = i - 1;
			while (topb && lt[i].y < stb[topb].y) {
				T.Update(1, 1, n, stb[topb].x, Next, lt[i].y - stb[topb].y);
				Next = stb[topb].x - 1; -- topb;
			}
			if (Next != i - 1) stb[++ topb] = mp(Next + 1, lt[i].y);
		}
		sta[++ topa] = mp(i, 0);
		stb[++ topb] = mp(i, h);

		T.Update(1, 1, n, i, i, h - lt[i].x);
		chkmax(ans, T.maxv[1] + lt[i + 1].x);
	}
}

int main () {
	File();
	w = read(); h = read(); n = read();
	For (i, 1, n) {
		lt[i].x = read();
		lt[i].y = read();
	}
	lt[++ n] = mp(0, 0);
	lt[++ n] = mp(w, h);
	Work();

	For (i, 1, n)
		swap(lt[i].x, lt[i].y);
	swap(w, h);
	Work();

	printf ("%d\n", ans << 1);
    return 0;
}