??? cliquers

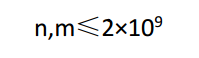
解：先推一个式子，然后就是CRT了...

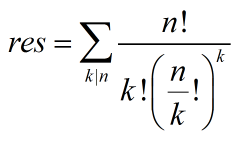
那个阶乘怎么求呢？主要是分母可能有0，这时我们把分母的因子p全部提出来，上下次数相减判断即可。

细节颇多......注意在快速幂开始的时候a %= MO是个好习惯。

 #include <cstdio>
 #include <algorithm>

 typedef long long LL;
 const int N = ;
 const LL MO = 1e9 - , mod[] = {, , , , };

 int turn;
 LL ans[], n, m, nn[][];
 //LL inv[10000][5], invn[10000][5];

 inline LL qpow(LL a, LL b, LL c) {
     LL ans = ;
     a %= c;
     while(b) {
         if(b & ) ans = ans * a % c;
         a = a * a % c;
         b = b >> ;
     }
     return ans;
 }

 inline LL Pow(LL a, LL b) {
     LL ans = ;
     while(b) {
         if(b & ) ans = ans * a;
         a = a * a;
         b = b >> ;
     }
     return ans;
 }

 LL exgcd(LL a, LL &x, LL b, LL &y) {
     if(!b) {
         x = ; y = ;
         return a;
     }
     LL g = exgcd(b, x, a % b, y);
     std::swap(x, y);
     y -= x * (a / b);
     return g;
 }

 inline LL getnn(LL x) {
     if(!x) return ;
     LL t = x / mod[turn];
     LL ans = qpow(nn[mod[turn] - ][turn], t, mod[turn]);
     t = x % mod[turn];
     return ans * nn[t][turn] % mod[turn] * getnn(x / mod[turn]);
 }

 inline LL cal(LL k) {

     //printf("cal %lld \n", k);
     //bool f = (turn == 2 && k == 2) || (turn == 2 && k == 1);

     LL time = ;
     for(LL i = n; i > ; i /= mod[turn]) {
         time += i / mod[turn];
         //printf("1 time += %lld  = %lld \n", i / mod[turn], time);
     }
     for(LL i = k; i > ; i /= mod[turn]) {
         time -= i / mod[turn];
         //printf("2 time -= %lld  = %lld \n", i / mod[turn], time);
     }
     for(LL i = n / k; i > ; i /= mod[turn]) {
         time -= (i / mod[turn]) * k;
         //printf("3 time -= %lld  = %lld\n", i / mod[turn], time);
     }
     if(time) {
         //printf(" -- -- return 0 \n");
         //printf("mod = %lld ans = 0\n", mod[turn]);
         return ;
     }

     LL t1 = getnn(n), t2 = getnn(k), t3 = getnn(n / k);
     /*if(f) {
         printf("%lld %lld %lld \n", t1, t2, t3);
     }*/
     t3 = qpow(t3, k, mod[turn]);
     t2 = qpow(t2, mod[turn] - , mod[turn]);
     t3 = qpow(t3, mod[turn] - , mod[turn]);

     //printf("return %lld \n", t1 * t2 % mod[turn] * t3 % mod[turn]);
     //printf("mod = %lld k = %lld ans = %lld \n", mod[turn], k, t1 * t2 % mod[turn] * t3 % mod[turn]);
     return t1 * t2 % mod[turn] * t3 % mod[turn];
 }

 inline LL solve() { /// cal each prime
     LL ans = ;
     for(LL i = ; i * i <= n; i++) {
         if(n % i) continue;
         ans = (ans + cal(i)) % mod[turn];
         if(i * i < n) {
             ans = (ans + cal(n / i)) % mod[turn];
         }
     }
     return ans;
 }

 inline void work() {
     scanf("%lld%lld", &n, &m);
     //m %= MO;

     for(turn = ; turn <= ; turn++) {
         ans[turn] = solve();
         //printf("ans %d %lld = %lld \n", turn, mod[turn], ans[turn]);
     }

     /// excrt
     /*LL a = ans[1], p = mod[1];
     for(int i = 2; i <= 4; i++) {
         /// merge
         //printf("merge %d \n", i);
         LL P = p * mod[i], x, y;
         LL c1 = ((a - ans[i]) % P + P) % P;
         //printf("a = %lld  c1 = %lld \n", a, c1);
         LL g = exgcd(mod[i], x, p, y);
         (x *= (c1 / g)) %= P; (y *= (c1 / g)) %= P;
         a = (x * mod[i] % P + ans[i]) % P;
         p = P;
         //printf("merge %lld ans = %lld \n", mod[i], a);
     }*/
     /// crt
     LL a = , p = MO - ;
     for(int i = ; i <= ; i++) {
         a = (a + ans[i] * (p / mod[i]) % p * qpow(p / mod[i], mod[i] - , mod[i]) % p) % p;
     }

     //printf("over \n");
     a = (a % p + p) % p;
     //printf("a = %lld\n", a);
     LL ans = qpow(m, a, MO);
     printf("%lld\n", ans);
     return;
 }

 inline void prework() {
     for(turn = ; turn <= ; turn++) {
         //invn[0][turn] = inv[0][turn]turn] = nn[0][turn] = 1;
         nn[][turn] = ;
         //invn[1][turn] = inv[1][turn]turn] = nn[1][turn] = 1;
         for(int i = ; i < mod[turn]; i++) {
             nn[i][turn] = nn[i - ][turn] * i % mod[turn];
             //inv[i][turn] = inv[mod[turn] % i] * (mod[turn] - mod[turn] / i) % mod[turn];
             //invn[i][turn] = invn[i - 1][turn] * inv[i][turn] % mod[turn];
         }
     }
     return;
 }

 int main() {

     freopen("cliquers.in", "r", stdin);
     freopen("cliquers.out", "w", stdout);

     prework();

     int T;
     scanf("%d", &T);
     while(T--) {
         work();
     }
     return ;
 }

AC代码

两种CRT都写了。