密码疑云 (2)——RSA加密机制需要的数学知识

　　在公钥密码体制提出不久，人们就找到其中的三种，其中最著名的当属RSA体制。RSA是一种非对称加密体制，在公开密钥加密和电子商业中被广泛使用。RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。当时他们三人都在麻省理工学院工作，RSA就是他们三人姓氏开头字母拼在一起组成的。

　　RSA背后的原理是一个数论理论——将两个大素数（比如1024位的素数）相乘很容易，但是想要对它们的乘积进行素因子分解（重新分解成原来的两个素数的乘积）却及其困难。在理解RSA之前还需要知道一些数学概念。

公约数定理和线性不定方程

　　公约数存在两个定理，如果d=GCD(a,b)则：

　　1. 存在整数x,y，使得d=ax+by，当然，x,y用不着全是正整数（贝祖定理）；

　　2. 如果c是a,b的另一个公约数，则c|d

　　定理2还产生了一个推论：GCD(a,b)是a,b的线性组合{ax+by}中的最小正元素。

　　根据公约数定理可以给出线性不定方程的定义：对于任意整数a,b,c，型如ax+by=c的方程称为线性不定方程，“线性”表示方程的未知数次数是一次，“不定” 表示未知数的个数多于方程的个数。如果c= GCD(a,b)，则方程存在一组整数解；如果c是GCD(a,b)的整数倍，方程存在多组整数解；否则方程无整数解。

　　通常使用欧几里德算法求解线性方程组ax+by=GCD(a,b)。欧几里德算法通过辗转关系求得两个数的最大公约数：

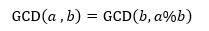
　　不断迭代，直到a%b=0为止：

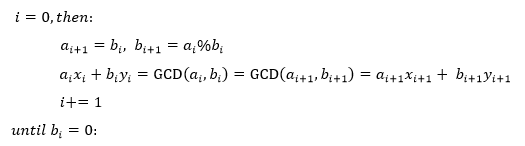
　　下标表示迭代次数，原方程是第0次迭代。

　　欧几里德算法（辗转相除）可参考整数的故事(2)——辗转相除与更相减损

　　最后一次迭代（第n+1次迭代）时，a_n%b_n=0：

　　其中的一组特解是x_n+1=1,y_n+1=0，虽然这组解并不是关于x₀和y₀的，但可以通过它反向推出原方程的解。

　　在Python中，a%b==a-(a//b)*b代入①中可以得到x_n=1,y_n与x_n+1=1,y_n+1的关系：

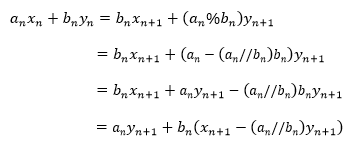
　　当x_n=1,y_n与x_n+1=1,y_n+1 满足下面关系时，上式是恒等式：

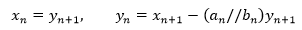
　　恒等式（identities）无论变量如何取值，等式永远成立。

　　这样就可以由x_n+1和y_n+1推出x_n和y_n，不断向前递推，最终可以求得x₀和y₀。下面的代码可求得原方程的解，被称为扩展欧几里德算法：

def extEculid(a, b):

    '''扩展欧几里德算法 计算 ax-by = GCD(a, b)的特解'''

    if b == 0:

        x, y = 1, 0

        return x,y

    x, y = extEculid(b, a % b)

    return y, x - (a // b) * y

if __name__ == '__main__':

    print('5x + 10y = 5', '=>', extEculid(5, 10))

    print('5x + 11y = 1', '=>', extEculid(5, 11))

    print('16x + 24y = 8', '=>', extEculid(16, 24))

    print('72x + 57y = 3', '=>', extEculid(72, 57))

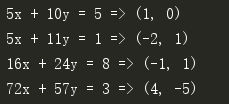
　　作为一种最简情况，对于ax+by=1来说，如果GCD(a,b) = 1，方程有唯一解。这是由ax+by=GCD(a,b)推导而来的：

　　由于d是a和b的最大公约数，所以a/d和b/d一定是整数，且它们之间不会再有其它约数（否则d就不是a和b的最大公约数）：

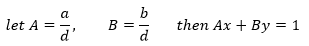
　　重新命名系数，用a,b代替A,B就可以得出结论。

　　如果在原方程中c是GCD(a,b)的整数倍，方程组有多组解，这些解是什么呢？

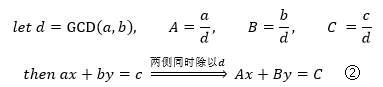
　　由于d已经是a,b的最大公约数，所以A,B不再有其它的约数，A,B互质于是不定方程③有唯一解：

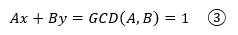
　　根据扩展欧几里德算法可以计算出它的唯一解，设这组解是x₀，y₀，将解代入③：

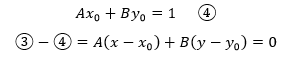
　　由A,B互质，因此x-x₀定有因子B，y-y₀一定有因子A，由此可以得到不定方程的通解：

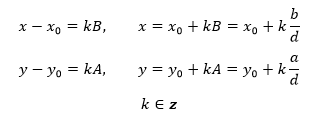
　　满足方程的解有无穷多个，在实际问题中我们常常只要求其最小正整数解。如果不考虑y的取值，的最小正整数解就是 x₀+kb/d>0时的最小值（注意是 x₀+kb/d的最小值，不是x₀的最小值）。

青蛙约会

　　一个圆形围墙下有两只青蛙A和B想要约会，它们的位置分别是x和y。它们高兴地出发了，但是出发前忘记了通知对方朝哪个方向前进。现在A、B同时沿着围墙的同一方向跳跃，A每次跳m，B每次跳n，场地的周长是L。假设两只青蛙跳跃一次的耗时相同，它们落在同一点视为相遇，那么它们经过几次跳跃才能相遇？

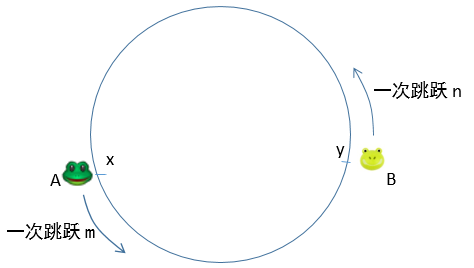
　　青蛙约会成功的第一个前提是m≠n，否则它们会永远跳下去。假设x和y相距很近，并且A跳跃的比较快，如果能够相遇，那么A一定会比B至少多跳一圈，也就是运动会上常说的“扣圈”。当然了，在A马上要追上B时，如果下一跳又正好跳到了B的前面，那么这一圈就白扣了，需要重新追赶。设它们经过t次跳跃能够相遇，相遇时A比B多跳了k圈，可以写出下面的式子：

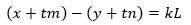
　　其中x,y,m,n,L是已知的，t,k是未知的，上式可以进一步转化为：

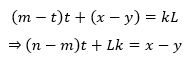
　　这和线性不定方程ax+by=c的形式一致。如果方程有整数解，那么x-y一定是GCD(n-m, L)的整数倍，此时可以根据扩展欧几里德算法求出线性方程的最小解。

同余、同余方程和乘法逆元

　　a和b是两个整数，如果它们的差a-b能够被另一个整数n整除，则称a，b对于模n同余，记作a≡b (mod n)，读作a与b关于模n同余（a is congruent to b mod n）。a≡b (mod n)的等价形式是当且仅当n|(a-b)，

　　a,b对于模可理解为a-b=kn，k是任意整数。当a≡0 (mod n)时，则n|a。

　　例如：

　　数学中被重用的符号很多，同余符号“≡”就是其中的一个。在几何中，“≡”也表示全等符号，△ABC和△A’B’C’全等，记作△ABC≡△A’B’C’，等同于△ABC≌△A’B’C’符号。在函数中，“≡”可以表示“恒等”，函数f(x)≡n表示该函数的值始终为n，与x的值无关。

　　同余问题很常见，例如从今天起计算n天和m天后是否是星期中的同一天？答案是当n≡m (mod 7)时。类似的例子还有很多，例如平面上位于同一顶点的两个线段，当各自朝同一方向旋转了n和m，当n≡m(mod 360°)时将重合；钟表上的时针从当前位置经过了n小时和m小时，当n≡m (mod 12)时会到达同一位置。

　　同余符号“≡”比等号“=”多了一横，它与等号具有的性质类似，允许两边同时加上或减去同一个量，或同时乘以一个常数，对于a≡b (mod n)，当c是整数时：

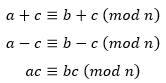
　　我们把型如ax≡b (mod n)的方程称为线性同余方程。在数论中，线性同余方程是最基本的同余方程，“线性”表示方程的未知数次数是一次。

　　同余方程的解有三种情况，只有当GDD(a, n)|b时，方程有解，例如：

　　1. 无解，例如2x≡1 (mod 4)；

　　2. 有唯一解，例如2x≡1 (mod 5)；

　　3. 有无数解，例如2x≡0 (mod 4)；

　　原方程是ax≡b (mod n)，则原方程的等价形式是：

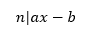
　　设y是一个指定的整数，则n能整除ax-b意味着：

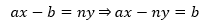
　　这就把同余方程转换成了线性不定方程ax+by=c的形式，可以用扩展欧几里德算法求解。当GCD(a, n)=b时，ax≡b (mod n)有唯一整数解。类似地，当b是GCD(a,n)的倍数时，同余方程有多组解。

　　作为最简情况，当ax-ny=1时，如果GCD(a,n)=1，则方程有唯一整数解，这个整数解就称为a在模n上的乘法逆元，记作a^-1：

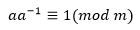
欧拉函数

　　对正整数n，欧拉函数（Euler's totient function）是小于n的正整数中与n互质的正整数的个数，用φ(n)表示。欧拉函数又称为φ函数、欧拉商数等，φ(n)的值被称为n的欧拉数。规定φ(1)=1。例如，在小于8的正整数中，1,3,5,7都与8互质，因此φ(8)=4，φ(8)是一个欧拉函数，它的值等于4，4是8的欧拉数。

　　当n是素数时，φ(n)=n-1，因为所有小于n的数都和n互素。

注：当年欧拉认可1是素数，所以在欧拉函数中1也被加了上去。下文在讨论欧拉函数时都把1视为素数。

　　欧拉函数有一个性质，如果n可以分解为两个互素正整数p和q的乘积，那么n的欧拉函数就是p和q的欧拉函数的乘积，即：

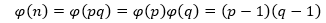
　　例如，小于12的正整数中与12互质的有1,5,7,11，所以φ(12)=4。12可以分解为两个互素的数3和4的乘积，因此：

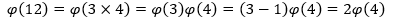
　　这里也许会产生一个冲动，把φ(4)继续写成φ(4)= 4-1，这是错误的，φ(n)=n-1的前提是n是素数，因此φ(4)≠4-1。另一个冲动是写成φ(4)= φ(2) φ(2)，这也是错误的，两个数互素的前提是它们的最大公约数是1，GCD(2,2)=2，因此2和2并不互素。

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

　　扫描二维码关注公众号“我是8位的”