codeforces Round #320 (Div. 2) C. A Problem about Polyline(数学) D. "Or" Game(暴力，数学)

解题思路：就是求数 n 对应的二进制数中有多少个 1

#include <iostream>
#include<cstdio>
using namespace std;  

int main(){
    int n;
    cin>>n;
    int ans = ;
//  while(n){//这也是一种好的方法
//      n = n&(n-1);
//      ++ans;
//  }

    while(n){
        if(n&) ++ans;
        n>>=;
    }
    cout<<ans<<endl;
    return ;
} 

解题思路:对（strength, i, j）按照strength进行递减排序，从左到右进行遍历，用b[N]表示i和j有关系！

如果发现b[i]或者b[j]有关系了，则跳过这个strength， 否则b[i] =j, b[j] = i;

#include <iostream>
#include <algorithm>
#include<cstdio>
using namespace std;  

struct node{
    int x;
    int i, j;
}a[];

int b[];

bool cmp(node a, node b){
    return a.x > b.x;
}

int main(){
    int x, n;
    int c = ;
    cin>>n;
    for(int k=; k<=*n; ++k){
        for(int kk=; kk<k; ++kk){
            cin>>x;
            a[c].x = x;
            a[c].i = k;
            a[c++].j = kk;
        }
    }
    sort(a, a+c, cmp);
    int cnt = ;
    for(int i=; i<c; ++i){
        if(!b[a[i].i] && !b[a[i].j]){
            b[a[i].i] = a[i].j;
            b[a[i].j] = a[i].i;
            ++cnt;
        }
        if(cnt == n) break;
    }
    for(int i=; i<=*n; ++i){
        if(i!=) cout<<" ";
        cout<<b[i];
    }
    cout<<endl;
    return ;
}

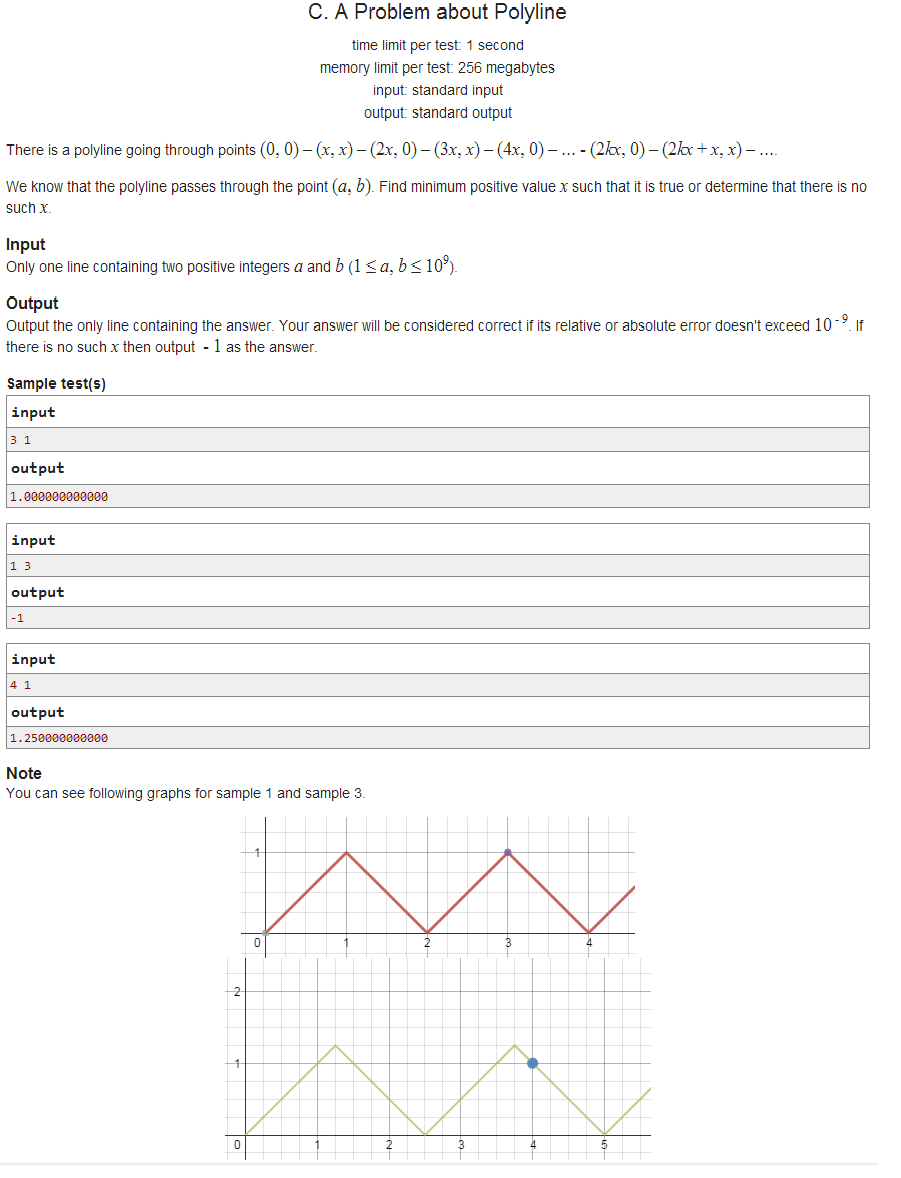
解题思路：

　

我们可以发现这样的一个规律：

(1)首先b一定要小于a，否则无论如何曲线也无法通过(a,b);

(2)设int k=a/b， 如果k为奇数，说明这个点在上图的绿色的线上， 没关系，我们让 k+=1；这样的话一定有(0,0), (a,b)这两点确定的直线的

斜率1/k介于(1/(k-1),  1/(k+1))之间，那么我们可以通过缩小（或者放大）X的值，使得第 k/2 个周期块 斜率为-1的那条边经过(a, b)。此时

的X值就是最小的！

(3)如果(a,b)在第 k/2 个周期块 斜率为-1的那条边上，那么这条边与X轴的交点就是(a+b, 0), 从(0, 0)到(a+b, 0)一共经过了 k/2个周期，

所以 X = (a+b)*1.0/(k/2 * 2)

(4)唉....想的这么明白，容易吗.....

#include <iostream>
#include <algorithm>
#include<cstdio>
#include<cmath>
using namespace std;  

int main(){
    int a, b;
    cin>>a>>b;
     if(b>a) {
         cout<<-<<endl;
     } else {
         int k = a/b;
         if(k&) ++k;
         printf("%.12lf\n", (a+b)*1.0/k);
     }
    return ;
}

解题思路：如果某个数a[i]乘以x， 必定会导致a[i]的二进制的长度增大。

首先求出或运算的前缀和后缀，然后对每个a[i]操作如下: a[i]*=x^k(x的k次方); 最后找到a[i]|pref[i-1]|suff[i+1]的最大值！

其实可以优化一处，就是a[i]|pref[i-1]|suff[i+1]的最大值一定对应二进制长度最大的a[i]; 可通过log(a[i])+1求得二进制长度！

#include <iostream>
#include <algorithm>
#include<cstdio>
#include<cmath>
#define N 200010
using namespace std;  

__int64 a[N];
__int64 pref[N];
__int64 suff[N];

int n, k, x;

int main(){
    scanf("%d%d%d", &n, &k, &x);
    long long maxN = ;
    for(int i=; i<=n; ++i)
        scanf("%I64d", &a[i]);
    long long xk = (long long)(pow((double)x, (double)k) + 0.5);
    for(int i=; i<=n; ++i){
        pref[i] = pref[i-] | a[i];
        suff[n-i+] = suff[n-i+] | a[n-i+];
    }

    for(int i=; i<=n; ++i){
        long long num = a[i]*xk | pref[i-] | suff[i+];
        if(maxN < num)
            maxN = num;
    }
    printf("%I64d\n", maxN);
    return ;
}