算法与数据结构基础 - 分治法(Divide and Conquer)

分治法基础

分治法(Divide and Conquer)顾名思义，思想核心是将问题拆分为子问题，对子问题求解、最终合并结果，分治法用伪代码表示如下：

function f(input x size n)
    if(n < k)
        solve x directly and return
    else
        divide x into a subproblems of size n/b
        call f recursively to solve each subproblem
　　Combine the results of all sub-problems            

分治法简单而言分三步 Divide、Conquer、Combine，图示如下：

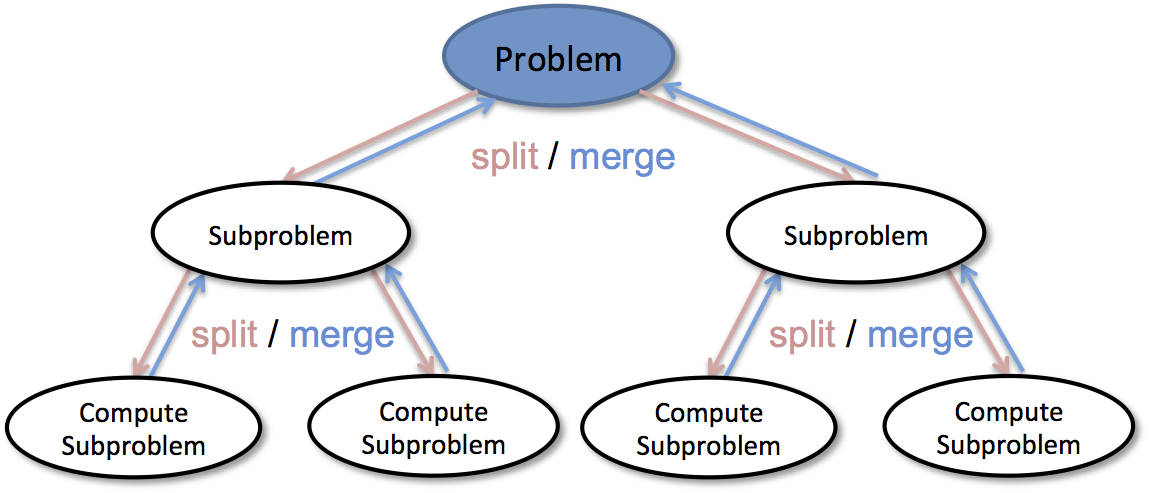
和动态规划、贪心等一样，分治法是一种算法思想，不是用于解决专门某类问题的方法。折半查找(Binary Search)、快速排序/快速选择/归并排序、二叉树处理等都包含了分治法的思想。

关于折半查找、快速排序/归并排序，详见：

算法与数据结构基础 - 折半查找(Binary Search)

算法与数据结构基础 - 排序(Sort)

相关LeetCode题：

169. Majority Element  题解

53. Maximum Subarray  题解

215. Kth Largest Element in an Array  题解

426. Convert Binary Search Tree to Sorted Doubly Linked List  题解

240. Search a 2D Matrix II  题解

218. The Skyline Problem  题解

4. Median of Two Sorted Arrays  题解

缓存过程结果(Memoization)

一些场景下我们会遇到相同的子问题，这时可以用哈希表等结构缓存子问题的结果，当再次遇到相同子问题时、直接返回结果即可，memoization是常用的减少计算复杂度的技巧。

相关LeetCode题：

241. Different Ways to Add Parentheses  题解

312. Burst Balloons  题解

时间复杂度

分治法中常用到递归，因而其时间复杂度并不直观，关于分治法时间复杂度计算，详见：

Advanced master theorem for divide and conquer recurrences