python机器学习——自适应线性神经元

上篇博客我们说了感知器，这篇博客主要记录自适应线性神经元的实现算法及一些其他的训练细节，自适应线性神经元（简称为Adaline）由Bernard Widrow和他的博士生Tedd Hoff提出，对感知器算法进行了改进。

当然Adaline对输入向量x的处理和感知器是一样的，都是使用一个权重向量w与x线性组合后得到z，再使用激活函数将z压缩到二元输入（1/-1），区别在于Adaline使用梯度下降法来更新w。

因为我们的目的是准确分类，那么我们需要来衡量分类效果的好坏，在这里我们介绍目标函数：
\[
J(w) = \frac12 \sum_i^n(y^i - \phi(z^i))^2
\]
它也可以叫做损失函数，通过上式我们可以大致理解为什么叫做损失函数，此函数可以计算出所有训练样本的真实值和预测值之间的误差平方和（Sum of Squared Errors，简称SSE），式子前面的那个1/2是为了之后求导方便添加的，没有其他意义。

有了损失函数，于是我们的目的更具体一点，就是为了选择合适的w，使损失函数取得最小值，损失函数越小，就意味着错误分类的情况越少，算法的分类效果也就越好。而因为Adaline的损失函数是一个凸函数，所以我们可以使用梯度下降来找到使损失函数取值最小的权重向量w，我们可以想象为一个小球滚下山：

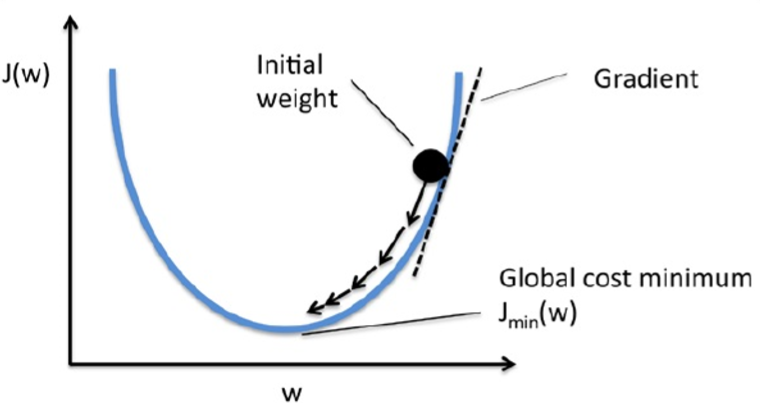
刚开始的w也许会得到一个很大的损失函数，但是由于损失函数J是w的函数，并且也是一个凸函数，它存在一个最小值，学过微积分的朋友应该知道，要找到一个函数的最值，一般的方法通过求导并使导数为零，解出的那个x就是最值，在这里的梯度下降也就是求导，但由于w是一个权重向量，是多维的，所以需要损失函数对w求偏导，得到w中每个分量的偏导数，然后再更新整个w，具体的推导过程如下：
\[
注意：w为向量，w_j为向量w中的某一分量\\w = w + \Delta w\\\Delta w = -\eta\Delta J(w)\\\frac{\partial J}{\partial w_j} = \frac{\partial }{\partial w_j} \frac 12 \sum_i(y^i-\phi(z^i))^2 \\= \frac 12 \frac{\partial }{\partial w_j} \sum_i(y^i-\phi(z^i))^2 \\= \frac 12 \sum_i2(y^i-\phi(z^i)) \frac{\partial }{\partial w_j}(y^i-\phi(z^i))\\= \sum_i(y^i-\phi(z^i))\frac{\partial }{\partial w_j}(y^i-\sum_i(w_j^ix_j^i))\\=\sum_i(y^i-\phi(z^i))(-x_j^i)\\=-\sum_i(y^i-\phi(z^i))x_j^i\\所以\Delta w_j = -\eta\frac{\partial J}{\partial w_j}=\eta\sum_i(y^i-\phi(z^i))x_j^i
\]
一点要注意所以的权重向量w中的分量是同时更新的，而且每次更新都用到了所有的训练样本，所以梯度下降法也被称为批量梯度下降（batch gradient descent）

接下来我们具体来实现自适应线性神经元，由于和感知机的学习规则很相似，所以直接在感知器的基础上进行修改得到，其中需要修改fit方法，因为在这里我们要使用梯度下降算法。

class AdalineGD(object):
    """ADAptive LInear NEuron classifier.
    Parameters
    ----------
    eta:float
        Learning rate(between 0.0 and 1.0
    n_iter:int
        Passes over the training dataset.
    Attributes
    ----------
    w_:1d-array
        weights after fitting.
    errors_:list
        Number of miscalssifications in every epoch.
    """
    def __init__(self, eta=0.01, n_iter=10):
        self.eta = eta
        self.n_iter = n_iter
    def fit(self, X, y):
        """Fit training data.
        :param X:{array-like}, shape=[n_samples, n_features]
        Training vectors,
        :param y: array-like, shape=[n_samples]
        Target values.
        :return:
        self:object
        """
        self.w_ = np.zeros(1 + X.shape[1]) # Add w_0
        self.cost_ = []
        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors ** 2).sum() / 2.0
            self.cost_.append(cost)
        return self
    def net_input(self, X):
        """Calculate net input"""
        return np.dot(X, self.w_[1:]) + self.w_[0]
    def activation(self, X):
        """Computer linear activation"""
        return self.net_input(X)
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.activation(X) >= 0.0, 1, -1)

分别使用不同的学习率（0.01和0.0001）训练，观察神经元学习过程。其中学习率、迭代次数我们称他们为超参数（hyperparameters），我们可以手动设置，超参数设置的是否合适对于整个训练过程都很重要。

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8,4))
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.show()

可以看出，左图中学习率为0.01，随着迭代次数的增加，误差在增加，说明学习率设置的不合适，产生了很大的危害，而右图学习率为0.0001，随着迭代次数的增加，误差在减少，但是减少的过于缓慢，算法收敛的很慢，训练的效率太低，所以我们可以看出过大或过小的学习率都是不合适的。

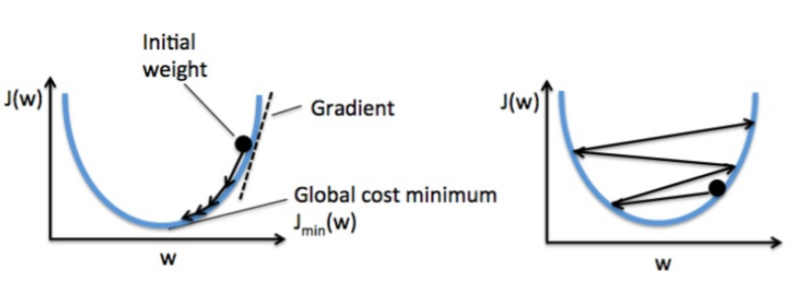
由右图可以看出，如果学习率过大，就会导致每次梯度下降时都跳过了对应最小值的权重向量w，使得算法无法收敛。

接下来我们介绍一种数据预处理方法，在训练前将特征进行某种缩放操作，这里我们称为特征标准化，可以使所有特征数据缩放成平均值为0，方差为1，加快模型的训练速度，而且可以避免模型学习的很扭曲。

具体公式如下：
\[
x_j^, = \frac {x_j-\mu_j}{\sigma_j}
\]
具体实现如下：

X_std = np.copy(X)

X_std[:, 0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()

X_std[:, 1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()

数据已经预处理结束，接下来我们开始训练模型

ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)

plot_decision_region(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.show()
plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epoches')
plt.ylabel('Sum-squared_error')
plt.show()

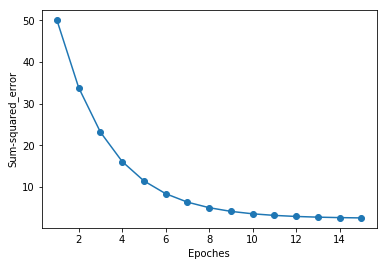
从上图看出，随着迭代次数的增加，误差逐渐降低，虽然学习率为0.01，在进行标准化之前，算法并不能收敛，但经过标准化后，算法最终收敛。