【题解】洛谷 P1014 【Cantor表】

1. 我们先引入三角形数的概念：
>定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为三角形数。

>古希腊著名科学家毕达哥拉斯把数1，3，6，10，15，21……这些数量的（石子），都可以排成三角形，像这样的数称为三角形数。

>【百度百科】三角形数

2. 我们来看看这个表：

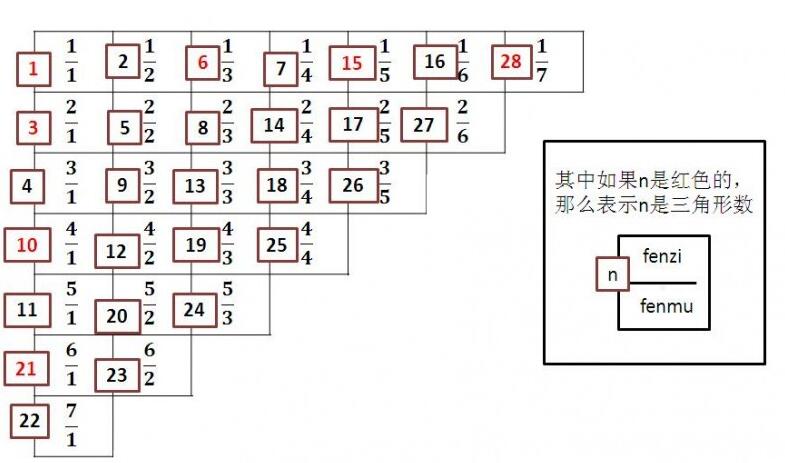
3. 我们可以发现，设
$x_1 < n \leqslant x_2$（其$x_1$、$x_2$均为三角形数）

即有$\dfrac{p(p-1)}{2} < n \leqslant \dfrac{p(p+1)}{2}$，其中$p \in Z$

也就是 $\begin{cases}p^2+p\geqslant2n……(1)\\p^2-p<2n……(2)\end{cases}$

对于(1)，我们有$p^2 + p + \dfrac{1}{4} \geqslant 2n + \dfrac{1}{4}$

配方得：

$(p+\dfrac{1}{2})^2 \geqslant 2n+\dfrac{1}{4}$

$\therefore p+\dfrac{1}{2}\geqslant \sqrt{2n+\dfrac{1}{4}}$ 或 $p+\dfrac{1}{2} \leqslant-\sqrt{2n+\dfrac{1}{4}}$

$\therefore p\geqslant \sqrt{2n+\dfrac{1}{4}}-\dfrac{1}{2}$ 或 $p\leqslant-\sqrt{2n+\dfrac{1}{4}}-\dfrac{1}{2}$

对于(2)，我们有$p^2 - p + \dfrac{1}{4} < 2n + \dfrac{1}{4}$

配方得：

$(p-\dfrac{1}{2})^2 < 2n+\dfrac{1}{4}$

$\therefore-\sqrt{2n+\dfrac{1}{4}}<p-\dfrac{1}{2}<\sqrt{2n+\dfrac{1}{4}}$

$\therefore-\sqrt{2n+\dfrac{1}{4}}+\dfrac{1}{2}<p<\sqrt{2n+\dfrac{1}{4}}+\dfrac{1}{2}$

为了方便，我们设$t=\sqrt{2n+\dfrac{1}{4}}$

$\therefore$联立得：$\begin{cases}p\geqslant t-\dfrac{1}{2} || p\leqslant- t - \dfrac{1}{2} \\-t+\dfrac{1}{2}<p<t+\dfrac{1}{2}\end{cases}$

解得：$t-\dfrac{1}{2}\leqslant p < t+ \dfrac{1}{2}$

又$\because t- \dfrac{1}{2}$到$t+\dfrac{1}{2}$中只可能有1个整数

$\therefore p= \lceil t- \dfrac{1}{2} \rceil$

4. 我们再来找规律

我们再设$\Delta s=x_2-n$

所以

当p为偶数时：要求的结果$\dfrac{p-\Delta s}{1+\Delta s}=\dfrac{p-x_2+n}{1+ x_2-n}$

化简后

分子是：$p-\dfrac{p(p+1)}{2}+n$

分母是：$1+\dfrac{p(p+1)}{2}-n$

当p为奇数时：要求的结果
$\dfrac{1+\Delta s}{p-\Delta s}=\dfrac{1+ x_2-n}{p-x_2+n}$

化简后

分子是：$1+\dfrac{p(p+1)}{2}-n$

分母是：$p-\dfrac{p(p+1)}{2}+n$

所以我们就有了这个代码：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <cmath>
 #include <cctype>
 #include <algorithm>
 #include <cstdlib>

 using namespace std;

 double t;
 int p, n;
 int fenzi, fenmu;

 int main()
 {
     scanf("%d", &n);
     t = sqrt( * n + 0.25);
     p = ceil(t - 0.5);
     if(p %  == )
     {
         fenzi = p - p * (p + ) /  + n;
         fenmu =  + p * (p + ) /  - n;
     }
     else
     {
         fenmu = p - p * (p + ) /  + n;
         fenzi =  + p * (p + ) /  - n;
     }
     printf("%d/%d", fenzi, fenmu);
     return ;
 }