MATLAB求解二重积分案例

凯鲁嘎吉 - 博客园

http://www.cnblogs.com/kailugaji/

定积分解决的是一维连续量求和的问题，而解决多维连续量的求和问题就要用到重积分了。重积分是建立在定积分的基础上的，它的基本思想也是将重积分化为定积分来计算，其中关键是积分限的确定，这也是重积分的难点所在。正是因为重积分从计算上来说仍是使用的定积分的方法，MATLAB系统并没有提供专门的命令函数来处理重积分，因此在我们确定了积分限后仍是使用int()命令来处理重积分问题。有些积分区间形状比较复杂，为了方便表达积分的上下限常常把比较复杂的区间分割成若干个相对简单的区间，然后对不同的区间分别积分，最后把各个积分结果相加起来。

计算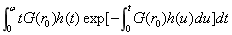

其中，

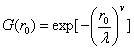
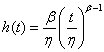
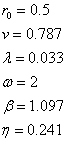
wrr.m:

function tt=wrr(r,v,c,b,y,w)
syms u t
p=-(r/c)^v;
g=exp(p);
h=(b/y)*(t/y)^(b-1);
hu=(b/y)*(u/y)^(b-1);
f=int(g*hu,u,0,t);
tt=int(t*g*h*exp(-f),t,0,w);
tt=vpa(tt,10);

//结果为：
>> clear
>> tt=wrr(0.5,0.787,0.033,1.097,0.241,2)

tt =

0.002183207532

对于二元函数的符号积分，可以先转化成逐次积分形式，利用int函数进行求解。