机器人路径规划其一 Dijkstra Algorithm【附动态图源码】

首先要说明的是，机器人路径规划与轨迹规划属于两个不同的概念，一般而言，轨迹规划针对的对象为机器人末端坐标系或者某个关节的位置速度加速度在时域的规划，常用的方法为多项式样条插值，
梯形轨迹等等，而路径规划针对的是机器人的一个整体如移动机器人或者无人机在已知或者未知的环境中规划其运动的路线，在slam机器人应用较多。然而两者的界限有时也有交叉，如机械臂末端工具运动到操作对象时需要避障以及规划时间时，也可以看作是路径规划问题。

常用的路径规划算法有Dijkstra, A*，D*, RRT, PRM以及在这些算法上演变的各种算法，这两天把Dijkstra Algorithm学习了下并用QT代码复现，所以本节先从Dijkstra讲起。Dijkstra是个人名，scientist Edsger W. Dijkstra 是个计算机科学家，这个算法的来源非常接地气，当时一天早上这位老哥和他的未婚妻在阿姆斯特丹逛街，然后在一个咖啡厅休息，休息的时候他在思考从城市鹿特丹到城市格罗宁根的最短路径问题，据他所述，这个算法被他在20分钟内想了出来，但是却在三年后才发表出来。

---

Ⅰ. 算法步骤

说明：把最短路径问题想象成一张图上某个起始点initial node到终点destination node的路径最短求解，图上除了起始点和终点还存在一些其它的可到达点以及无法达到点(障碍物)，每两个点之间都有一条权重不同的路径Edge，计每个点到起始点的路径长度为该点的距离的cost

1. 标记所有节点node为未访问状态unvisited（未访问节点集合），程序里一般给这些节点的cost设置为一个足够大的数。并建立一个{未访问节点集合}和{已接触节点集合}，以及{已访问节点集合}。

2. 设置起始点为迭代的第一个点，命名为current node，该点的cost显然为应该设置为0，将其纳入{已接触节点集合}。

3. 在每一次迭代中，对于当前的节点current node，计算所有与该节点能直接相连（相邻）的节点到该节点的距离hCost，如果 newCost=[hCost+(current node).cost] 比某一个相邻的节点的原先cost要小，则将该相邻的节点的cost更新为newCost，否则不做改变。将所有更新完cost的相邻节点纳入到{已接触节点集合}。

4. 当遍历完current node所有相邻的节点后，将current node节点从{已接触节点集合}中移除，并纳入到{已访问节点集合}。处于{已访问节点集合}的节点将不会在进入迭代计算过程。

5. 进入下一步迭代，新的current node从{已接触节点集合}选出，选择cost最小的那一个。

6. 如果目标点destination node被纳入{已访问节点集合}（代表最短路径已经找到）或者{已接触节点集合}中的所有点的cost都无穷大（代表找不到路径，有障碍），则迭代终止。

为了更好的理解上述步骤，可以参考以上的配图，上图是我从维基百科上截取的，感觉比我自己做的动画(后文贴出)要好，上图中，红色渐变点为visited nodes，即属于{已访问节点集合}，蓝色点为{已接触节点集合}，这些蓝色点原本为白色背景(未访问节点集合)，由于current node的每一次迭代更新，更新了相应的cost后被归类为已接触点，之后在下一次迭代中作为新的current node的预备种子集合，如果其中某个点cost最小，将会被选中称为current node，在迭代中最终会变成visited node，而只有visited node才能有机会称为最短路径中的一点，可谓是过五关斩六将。当迭代终止后，我们就需要从{已访问节点集合}中选中一组构成最短路径的节点集合，这里需要提前将节点node的数据结构定义好，显然的是，如果迭代找到了最终节点并停止了下来，那么最终节点会被存储进{已访问节点集合}，我们从最终节点开始回溯，最终节点的上一个节点应该是哪一个？这就需要在节点node的数据机构中提前定义好一个parent id的数据成员变量，在每个迭代步骤中的第3步，如果相邻的节点满足更新cost的条件，我们就将该相邻的节点成员中的parent id赋值为current node的id，没错，node数据结构除了parent id，还应该有一个唯一标识自身的id，这中结构类似于单向链表，按照这个步骤回溯到起始点，最短路径也就找到了。

那么该如何验证算法的正确性呢？

设想，在每一次迭代中，current node都是已接触节点中离起始节点最近的那个点，如果说我们找到的最短路径不是真正的最短路径的话，即最终节点d的父节点不是我们找到的最短路径的倒数第二个节点v，而是另外一个节点w，那么d的cost应该被更新为w.cost+dist[w2d]，d的父节点应该被相应更新为w，而不是v，与实际相矛盾，依次类推，可证。

Ⅱ. 程序实现

为了便于可视化实时的迭代过程，利用Qt的Qpainter在QWidger空间上通过定时器每隔一段时间暂停重启迭代过程，随机生成一个二维的图，二维矩阵中的每个元素的值对应于不同的节点，如0代表未访问，2代表已接触，6代表已访问等等，程序中因为设计到cost进行排序，需要用到priority queue加快速度，Dijkstra核心代码如下：

github源码：https://github.com/ShieldQiQi/Path-Planning-Showed-By-Animation

 1     start_ = start_in;
 2     goal_ = goal_in;
 3     n = grid.size();
 4
 5     // Get possible motions--> right, down and left, up
 6 //    std::vector<Node> motion = GetMotion();
 7     // set the start_ node as the current vertex
 8     open_list_.push(start_);
 9     //qDebug()<<open_list_.top().cost_<<" "<<open_list_.top().h_cost_;
10
11     // Main loop
12
13     SetTimer(NULL, 0, 50, (TIMERPROC)TimerProc);
14
15     while (!open_list_.empty())
16     {
17         // get the minist-cost node as a new one in each iteration
18         Node current = open_list_.top();
19         open_list_.pop();
20         // assign the order as the id
21         current.id_ = current.x_ * n + current.y_;
22
23         // find if current is the goal node
24         if (CompareCoordinates(current, goal_))
25         {
26             // if yes, than the work is done and exit
27             closed_list_.push_back(current);
28             grid[current.x_][current.y_] = 2;
29             KillTimer(NULL, 0);
30             return closed_list_;
31         }
32         grid[current.x_][current.y_] = 2;  // Point opened
33
34         // find all the neighbours and update their distance to the original node
35         for (const auto& m : motion)
36         {
37             Node new_point;
38             //qDebug()<<new_point.cost_<<" "<<new_point.h_cost_;
39             //qDebug()<<m.cost_<<" "<<m.h_cost_;
40             new_point = current + m;
41             //qDebug()<<new_point.cost_<<" "<<new_point.h_cost_;
42
43             new_point.id_ = n * new_point.x_ + new_point.y_;
44             new_point.pid_ = current.id_;
45
46             if (CompareCoordinates(new_point, goal_))
47             {
48                 open_list_.push(new_point);
49                 break;
50             }
51             // Check boundaries
52             if (new_point.x_ < 0 || new_point.y_ < 0 || new_point.x_ >= n || new_point.y_ >= n)
53             {
54                 continue;
55             }
56             // obstacle or visited
57             if (grid[new_point.x_][new_point.y_] != 0)
58             {
59                 continue;
60             }
61             // push all the mearsured node into a priority queue which the minist-cost one will be in the top
62             open_list_.push(new_point);
63         }
64         closed_list_.push_back(current);
65         // update the grid to get a dynamic-view
66
67     }
68
69     KillTimer(NULL, 0);
70
71     // no solution founded
72     closed_list_.clear();
73     Node no_path_node(-1, -1, -1, -1, -1, -1);
74     closed_list_.push_back(no_path_node);

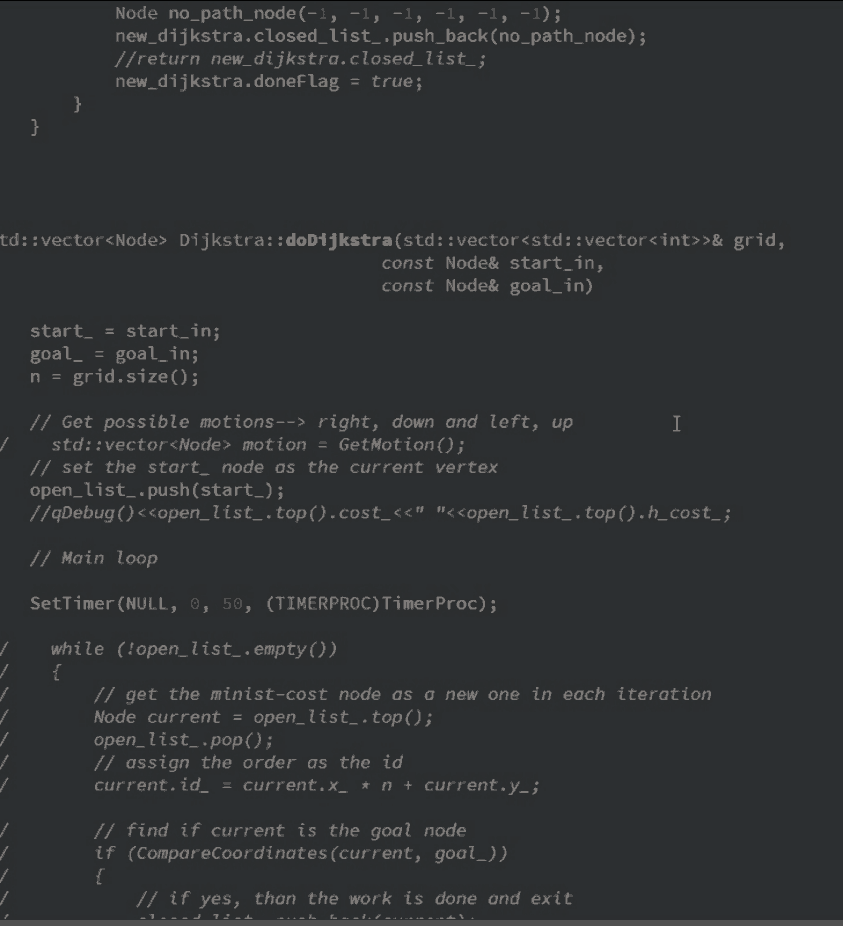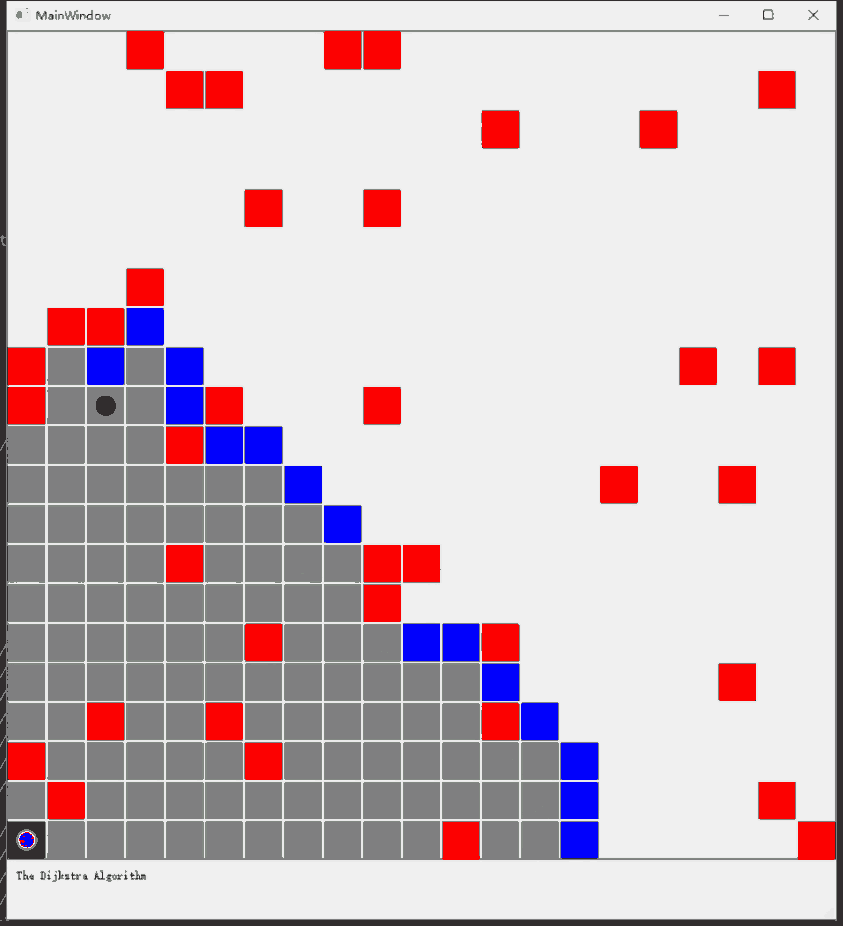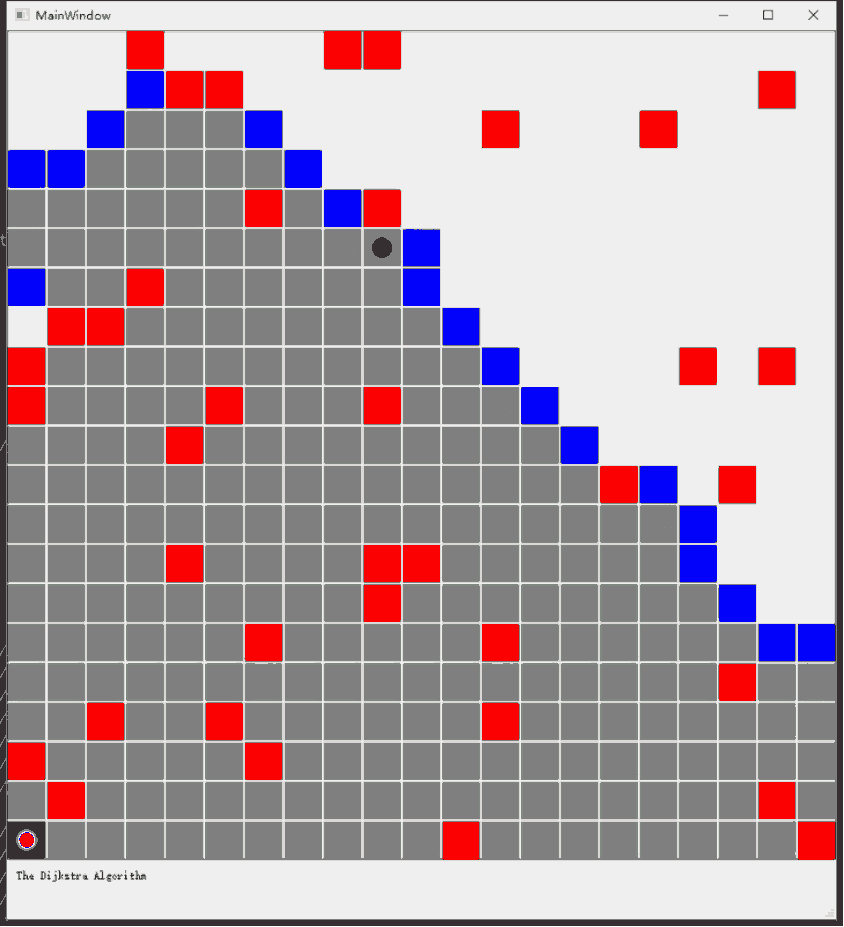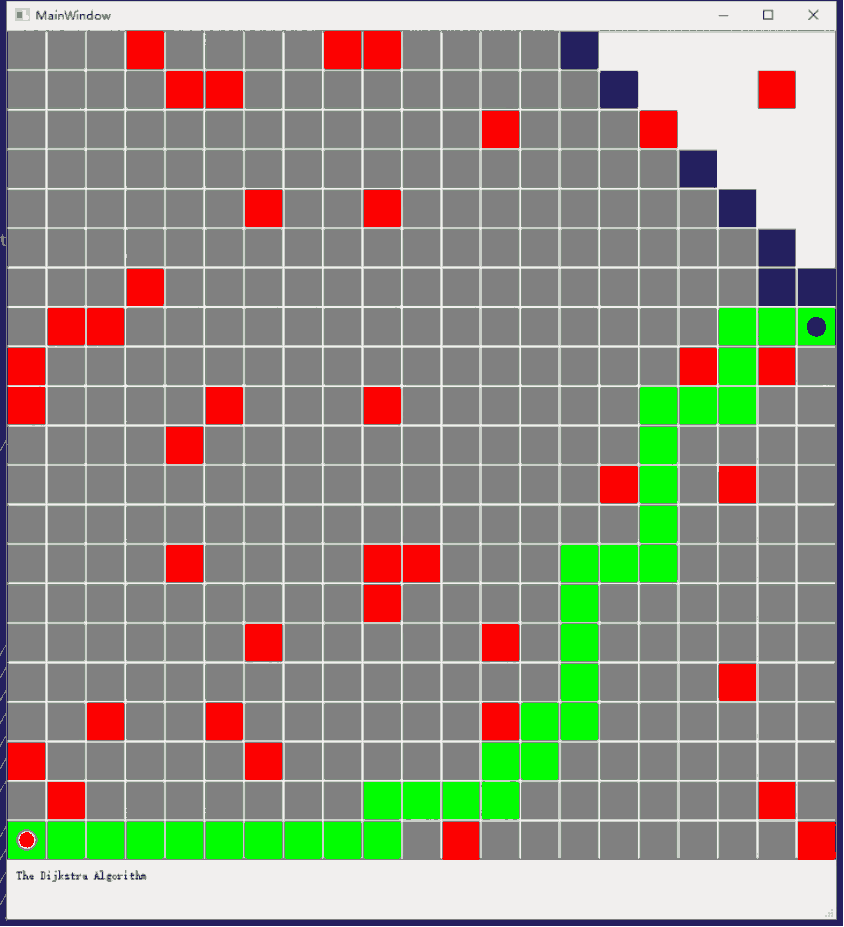
Ⅲ. 迭代过程动画

因为设置的运动方向只有上下左右，所以最终的路径是不能走斜线的，如果设置成斜线，最短路径可以视觉上更短，下图中，灰色方块表示visited nodes，蓝色代表已接触，红色代表障碍物，最终的规划路径用绿色方块表示：

Reference:

[1] https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm#Applications\

[2] https://github.com/vss2sn/path_planning