图的遍历BFS广度优先搜索

图的遍历BFS广度优先搜索

1. 简介

BFS（Breadth First Search，广度优先搜索，又名宽度优先搜索），与深度优先算法在一个结点“死磕到底“的思维不同，广度优先算法关注的重点在于每一层的结点进行的下一层的访问。

2. BFS算法介绍

BFS算法和核心思路就是：从某个点一直把其邻接点走完，然后任选一个邻接点把与之邻接的未被遍历的点走完，如此反复走完所有结点。类似于树的层序遍历。

BFS的核心就是要把当前在哪作为一个状态存储，并将这个状态交给队列进行入队操作，故而，

算法步骤（用队列实现）

a) 访问指定起始点。

b) 访问当前顶点的邻接顶点有未被访问的顶点，并将之放入队列中。

c) 删除队列的队首节点。访问当前队列的队首，前面的步骤。直到队列为空。

d) 若若途中还有顶点未被访问，则再选一个点作为起始顶点。重复前面的步骤。（针对非连通图）。

3. 案例图示

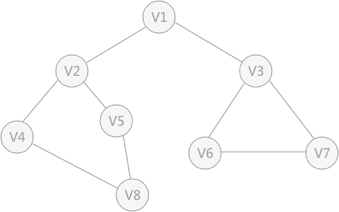
4. 相关代码

BFS的模板代码如下：

/**
 * 返回合适的检索数据
 */
int BFS(Node root, Node target)
{
    Queue<Node> queue;  //创建队列
    int step = 0;       // 当前队列的步骤点
    // initialize
    add root to queue;
    // BFS
    while (queue is not empty)
    {
        step = step + 1;
        //步数逐渐增加
        int size = queue.size();
        for (int i = 0; i < size; ++i)
        {
            Node cur = the first node in queue;
            if cur is target
                return step - 1;
            for (Node next : the neighbors of cur)
            {//这里常用一个二维方向数组实现
                add next to queue;
            }
            remove the first node from queue;
        }
    }
    return -1;          //出错返回值
}

完整代码：

#include<iostream>
using namespace std;
#define matrix_size 20
typedef struct {
    int weight;
}AdjMatrix[matrix_size][matrix_size];

struct  Queue{
    int data;
    Queue* next;
};

struct MGraph{
    int vex[matrix_size];
    AdjMatrix arcs;
    int vexnum,arcnum;
};
bool visited[matrix_size];    

int LocateVex(MGraph *G ,int v){
    int i;
    for ( i = 0; i < G->vexnum; i++)
    {
        if (G->vex[i]==v)
        {
            break;
        }
    }
    if (i>G->vexnum)
    {
        cout<<"not such vertex"<<endl;
        return -1;
    }
    return i;
}
//构造无向图
void CreateDN(MGraph *G){
    cin>>G->vexnum>>G->arcnum;
    for (int i = 0; i < G->vexnum; i++)
    {
        cin>>G->vex[i];
    }
    for (int i=0; i<G->vexnum; i++) {
        for (int j=0; j<G->vexnum; j++) {
            G->arcs[i][j].weight=0;
        }
    }
    for (int i = 0; i < G->arcnum; i++)
    {
        int v1,v2;
        cin>>v1>>v2;
        int n=LocateVex(G,v1);
        int m=LocateVex(G,v2);
        if (m==-1||n==-1)
        {
            cout<<"not this vertex"<<endl;
            return ;
        }
        G->arcs[n][m].weight=1;
        G->arcs[m][n].weight=1;
    }

    return ;
}
//输出函数
void PrintGrapth(MGraph G)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        for (int j = 0; j < G.vexnum; j++)
        {
            cout<<G.arcs[i][j].weight<<" ";
        }
        cout<<endl;
    }
}
void visitVex(MGraph G,int v){
    cout<<G.vex[v]<<" ";
}
int FirstAdjVex(MGraph G,int v){
    for (int i = 0; i < G.vexnum; i++)
    {
        //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
        if (G.arcs[v][i].weight)
        {
            return i;
        }
    }
    return -1;
}
int NextAdjVex(MGraph G,int v,int w)
{
    //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
    for(int i = w+1; i<G.vexnum; i++){
        if(G.arcs[v][i].weight){
            return i;
        }
    }
    return -1;
}

Queue* InitQueue(){
        Queue* Q=new Queue;
        Q->next=NULL;
        return Q;
}

//顶点元素v进队列
void EnQueue(Queue * Q,int v){
    Queue *element = new Queue;
    element->data=v;
    element->next=NULL;
    Queue* temp=Q;
    while (temp->next!=NULL)
    {
        temp=temp->next;
    }
    temp->next=element;
    // cout<<"in enqueue "<<element->data<<" ";
}

//队头元素出队列
Queue * DeQueue(Queue *Q,int *u){
    (*u)=Q->next->data;
    Q=Q->next;
    return Q;
}

//判断队列是否为空
bool QueueEmpty(Queue *Q){
    if (Q->next==NULL)
    {
        return true;
    }
    return false;
}

//广度优先搜索
void BFSTraverse(MGraph G){
    int v;
    for ( v = 0; v < G.vexnum; v++)
    {
        visited[v]=false;
    }
    Queue * Q;
    Q=InitQueue();
    for (v=0 ; v <G.vexnum ; v++)
    {
        if (!visited[v])
        {
            visited[v]=true;
            visitVex(G,v);
            EnQueue(Q,G.vex[v]);
            while (!QueueEmpty(Q))
            {
                int u;
                Q=DeQueue(Q,&u);
                u = LocateVex(&G,u);
                for (int w=FirstAdjVex(G, u); w>=0; w=NextAdjVex(G, u, w)) {
                    if (!visited[w]) {
                        visited[w]=true;
                        visitVex(G, w);
                        EnQueue(Q, G.vex[w]);
                    }
                }

            }

        }
    }

}

int main() {
    MGraph G;//建立一个图的变量
    CreateDN(&G);//初始化图
    BFSTraverse(G);//广度优先搜索图
    return 0;
}

结果：

8 9
1 2 3 4 5 6 7 8
1 2
2 4
2 5
4 8
5 8
1 3
3 6
6 7
7 3
1 2 3 4 5 6 7 8