leetcode 51. N皇后 及 52.N皇后 II

51. N皇后

问题描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

问题分析

当在棋盘上放置了一个皇后后，立即排除当前行，列和对应的两个对角线。即：

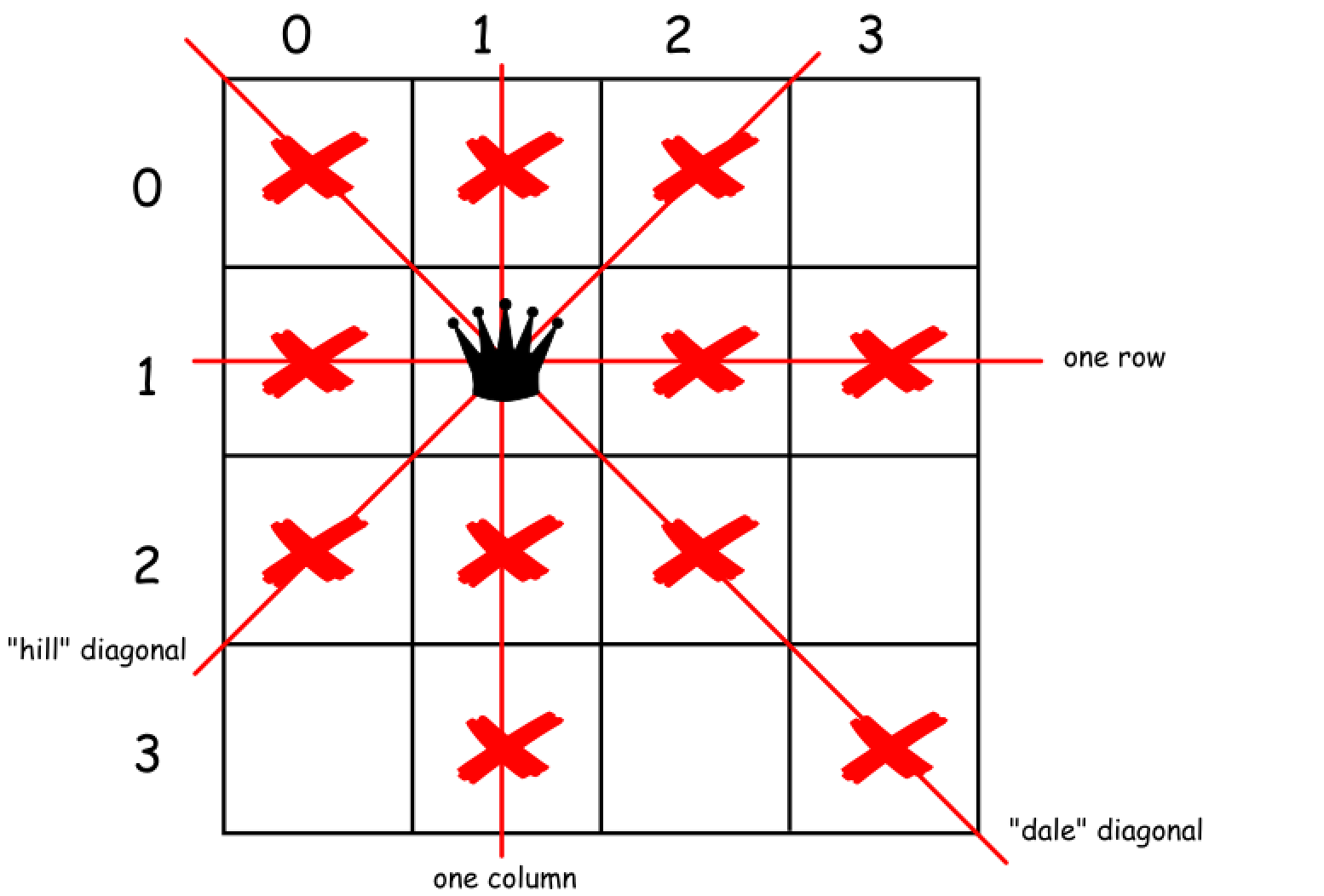
代码

class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<string> path(n,string(n,'.'));
        vector<vector<string>> ans;
        backtrack(n,0,ans,path);
        return ans;
    }
    void backtrack(int n,int row,vector<vector<string>> &ans,vector<string> &path)
    {
        if(row == n)
        {
            ans.push_back(path);
            return;
        }
        for(int i = 0; i < n; ++i)
        {
            if(checkvaild(n,row,i,ans,path))
            {
                path[row][i] = 'Q';
                backtrack(n,row+1,ans,path);
                path[row][i] = '.';
            }
        }
    }
    bool checkvaild(int n,int row,int col,vector<vector<string>> &ans,vector<string> &path)
    {
        int i,j;
        for(i = 0; i < row; i++)
        {
            if(path[i][col] == 'Q')return false;
        }
        for(i = row - 1,j = col - 1;i>=0&&j>=0;--i,--j)
        {
            if(path[i][j] == 'Q')return false;
        }
        for(i = row - 1,j = col + 1;i>=0&&j<n;--i,++j)
        {
            if(path[i][j] == 'Q')return false;
        }
        return true;
    }
};

结果：

执行用时 :12 ms, 在所有 C++ 提交中击败了62.59%的用户
内存消耗 :9.5 MB, 在所有 C++ 提交中击败了100.00%的用户

52.N皇后 II

问题描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

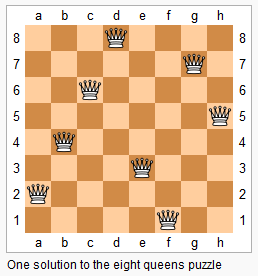
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

代码

class Solution {
public:
    int totalNQueens(int n) {
        vector<string> path(n,string(n,'.'));
        int num = 0;
        backtrack(n,0,path,num);
        return num;
    }
     void backtrack(int n,int row,vector<string> &path,int& num)
    {
        if(row == n)
        {
            ++num;
            return;
        }
        for(int i = 0; i < n; ++i)
        {
            if(checkvaild(n,row,i,path))
            {
                path[row][i] = 'Q';
                backtrack(n,row+1,path,num);
                path[row][i] = '.';
            }
        }
    }
    bool checkvaild(int n,int row,int col,vector<string> &path)
    {
        int i,j;
        for(i = 0; i < row; i++)
        {
            if(path[i][col] == 'Q')return false;
        }
        for(i = row - 1,j = col - 1;i>=0&&j>=0;--i,--j)
        {
            if(path[i][j] == 'Q')return false;
        }
        for(i = row - 1,j = col + 1;i>=0&&j<n;--i,++j)
        {
            if(path[i][j] == 'Q')return false;
        }
        return true;
    }
};

结果：

执行用时 :4 ms, 在所有 C++ 提交中击败了89.95%的用户
内存消耗 :8.5 MB, 在所有 C++ 提交中击败了30.71%的用户

参考链接